4 crucial tests LK-99 must pass to be a true superconductor

Every time a new claim comes along that would change the world, the first thing any respectable scientist needs to ask themselves is, “Is this claim true?” Perpetual motion machines promise free, unlimited energy, but the problem is that they’re not physically real. It would change the world if planet Earth had been visited by intelligent aliens, but the problem is there exists no good evidence that this has ever occurred. And, similarly, the idea of transmitting electricity with no resistance or heat loss would also change the world. This is physically possible under the conditions of a superconductor — first discovered way back in 1911 — but practically, has only been achieved at low temperatures and/or exceedingly high pressures.

Unless, that is, the new claims about a material known as LK-99 turn out to be true. Theorized, synthesized, and tested by South Korean scientists Sukbae Lee and Ji-Hoon Kim, they uploaded two preprint papers asserting that they had found the first room temperature, ambient pressure superconductor, and had demonstrated both zero resistance and the magnetic levitation phenomenon associated only with superconductors: the Meissner effect.

But is LK-99 really what they say it is? Are the claims of its superconductivity true? Here are the four key questions we should all be asking and that replication efforts should all be focused on answering.

When cooled to low enough temperatures, certain materials will superconduct: the electrical resistance inside them will drop to zero. When exposed to a strong magnetic field, some superconductors will exhibit levitation effects, and with a properly configured external magnetic field, it’s possible to “pin” the superconducting object in place in one or more dimensions, resulting in spectacular applications like quantum levitation. This has not yet been demonstrated for LK-99.

1.) Can we see the voltage across this material drop toward zero, as expected for a superconductor?

When you have an actual superconductor, what you typically see is that, as you decrease the temperature from a non-superconducting state, the resistance gradually drops. Then, once you reach a critical temperature, the resistance all of a sudden absolutely plummets: down to zero. Not near zero or close to zero, but to exactly zero. Above that critical temperature, this is just a normal material: with a non-zero resistivity, and therefore, because of its finite thickness and length, a non-zero resistance, and therefore obeys Ohm’s Law for the relationship between voltage, current, and resistance: V = IR.

However, below that critical temperature, the resistance should disappear completely. Not “drop at a different rate” but rather plummet down to zero very rapidly, and then remain at zero — at exactly zero — for all temperatures below that critical value. That means, if you graph resistance (or resistivity) for the material as a function of temperature, you should see that resistance plummet to zero. As a consequence of that, if you create a graph of voltage vs. current, you should see voltage and current be proportional to one another during non-superconducting conditions, but when it is superconducting, voltage should remain zero irrespective of what the value for current is.

This graph, from Lee and Kim’s first paper on LK-99, shows the applied current (x-axis) versus the measured voltage (y-axis) across their LK-99 sample at several different temperatures. The y-axis is displayed at insufficient resolution to tell whether the voltage truly goes to zero or is merely small, and the lack of any data points along the vertical lines, which should show the transition to a superconducting state, are serious omissions that should raise the hackles of anyone inclined toward skepticism about this result.

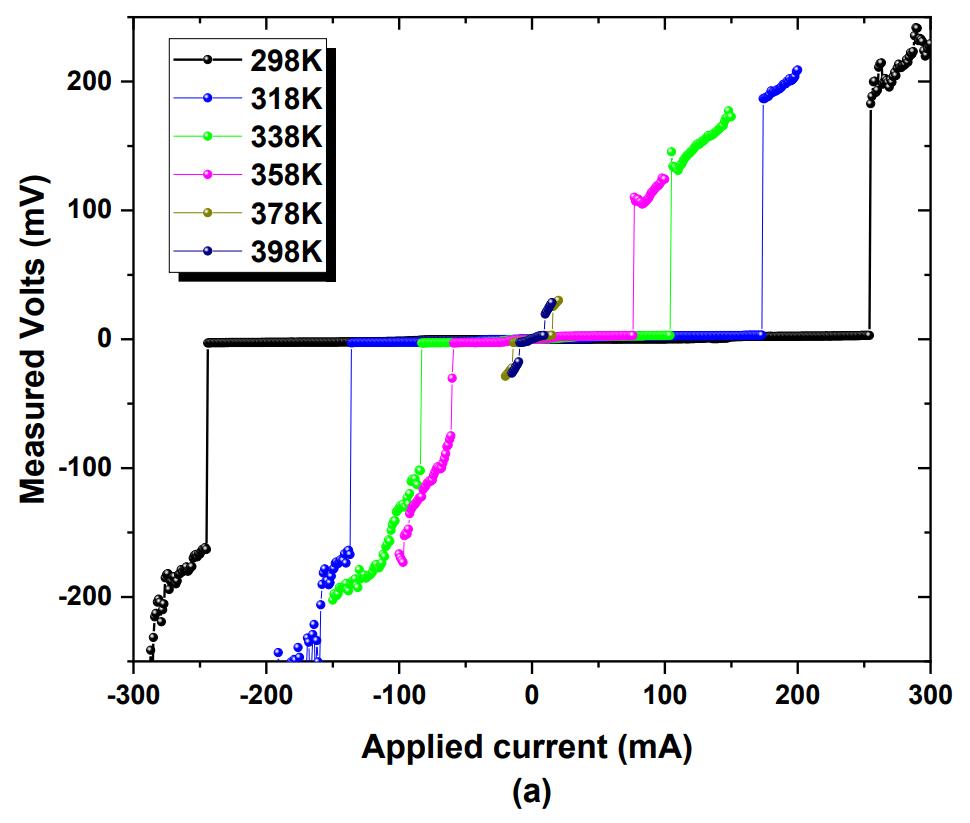
Above, you can see a figure from the first paper that Lee and Kim (and another collaborator, Young-Wan Kwon) uploaded on July 22, 2023, that shows voltage versus current. What you can clearly see is that there are conditions at large enough currents where the voltage changes as a function of current: evidence of significant resistance. At small currents (and how small they need to be appears to show a temperature dependence), however, the voltage appears to be consistent with zero, which is what you’d expect if V = IR where R = 0. You’d get that V = 0, irrespective of what the current is, because R = 0 implies V = 0.

But one of the things that’s missing from this graph is the key set of data points that you’d need to illustrate the transition: the data points where the voltage drops to zero, i.e., along those near-vertical lines. Those data points are simply not there, highlighting a key piece of evidence that’s absent from their work: the demonstrated transition between non-superconducting and actually superconducting behavior. All that they’ve shown is that, below a certain applied current in a temperature-dependent fashion, the resistivity of the material abruptly changes, not that it goes to zero. Those key data points are necessary to demonstrate the transition to superconductivity, and their absence is incredibly frustrating.

Although this graph does show, from Lee and Kim’s first paper in 2023, a measured voltage that’s indistinguishable from zero across this allegedly superconducting sample, it only does so for very, very small applied currents, far away from the limits of where their sample appears to stop exhibiting the desired behavior. That is consistent with evidence for a superconductor, but also just for a good conductor at very low currents.

2.) Does the voltage actually drop all the way to zero, or does it just drop significantly to a small but non-zero value?

This is a big worry: does the voltage across this material actually drop all the way to zero, indicating a transition to superconductivity, or does it simply drop from a larger value to a smaller value that looks consistent with zero due to the size of the vertical axis?

The reason this is such an important question to ask is because there are plenty of materials that are bad conductors under some conditions (temperature, pressure, or arrangement of atoms) that become good conductors when those conditions differ. This is known as a metal-insulator transition, and could be tricking Lee and Kim into thinking that their material is superconducting when, in fact, it’s just exhibiting the low-resistance properties of a normal run-of-the-mill conductor.

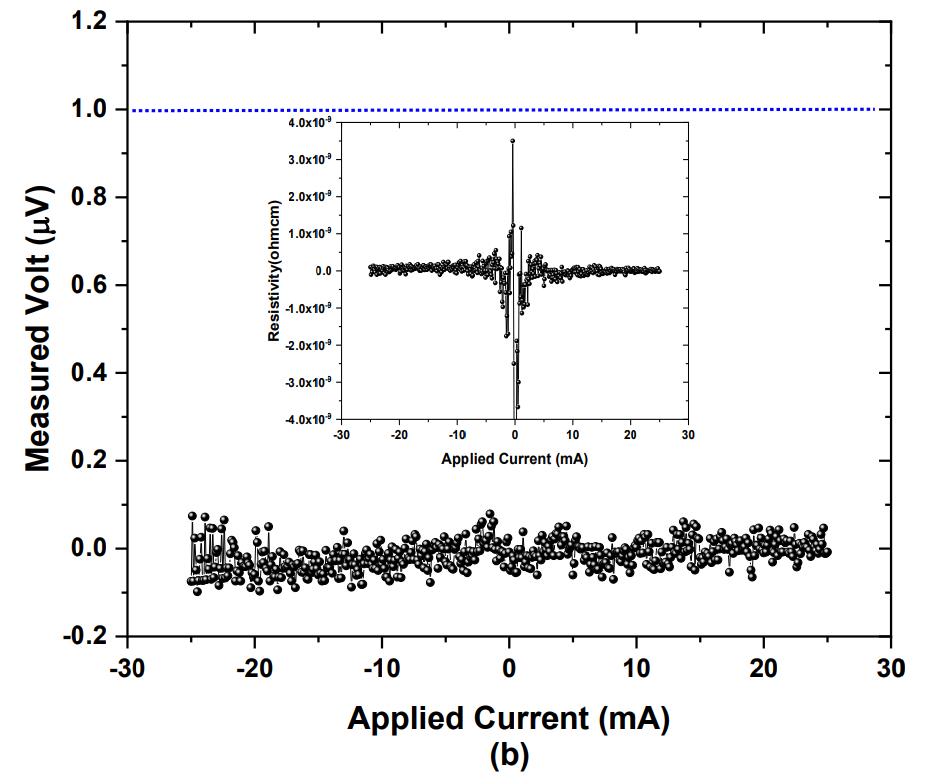
Above, you can see a graph from the first Lee & Kim paper (with Kwon as well) that appears to show that the voltage is truly zero, but this is suspicious because it only appears for the absolutely lowest applied currents: currents that are at tens of milliamps, rather than the hundreds of milliamps where the alleged transition (either to superconductivity or low resistivity) occurs.

This figure, extracted and horizontally stretched from the second of Lee and Kim’s papers on LK-99, clearly shows that the voltage across their sample, below a certain value of applied current, doesn’t drop to zero, but rather drops to a small, positive, non-zero value: evidence that this is behaving only as a conductor, not as a superconductor.

But in the second paper with four additional coauthors, the critical data actually exists (shown above), and it’s actually quite damning. As you can see, the “voltage dropping to zero” data points are still nowhere to be found, meaning that problem #1 still remains a very valid concern. But very importantly, below what they’re calling the critical temperature, you still have what’s very clearly a positive, non-zero voltage when you apply even small currents. As you can see from the above graph, “voltage” for the y-axis doesn’t drop to zero, but rather to something like 2 or 3 millivolts, with a slight current dependence as well.

This is evidence that the resistivity does appear to change all at once, but that it does not drop all the way to zero, which is absolutely mandatory to claim that you’ve found a superconductor. Now, it’s possible that this material they made really does superconduct and is simply so impure that the low resistance we are seeing is because of the impurities present within it; this is why verification is required. But the simplest explanation is that there isn’t superconductivity at all, and this material is simply behaving as a very low-resistance material consistent with that of a normal conductor. The burden of proof is on them to show superconductivity, however, not the other way around.

This graph shows resistance versus temperature for a sample of yttrium barium copper oxide: the first material, discovered in the 1980s, to superconduct at temperatures greater than that of liquid nitrogen (77 K). Measuring many data points along the transition at the critical temperature is key to identifying a superconducting state, as is measuring precisely zero resistance at temperatures below that critical temperature. This reproduction of those results were done by undergraduate students at the University of Toronto.

3.) Does the resistivity itself, which can be directly measured, actually drop all the way to zero below a critical temperature?

Rather than use voltage as a proxy to infer that a state of zero resistance may have been achieved, why not just measure resistivity directly? After all, this can be done, and would be the most direct test of superconductivity that one could perform.

The first paper from Lee and Kim, perhaps curiously, omits this key measurement entirely. They title their paper “The First Room-Temperature Ambient-Pressure Superconductor” but do not present the zero resistance/resistivity measurements that would be the direct indicator of superconductivity, relying on the proxy measurements of voltage vs. current instead.

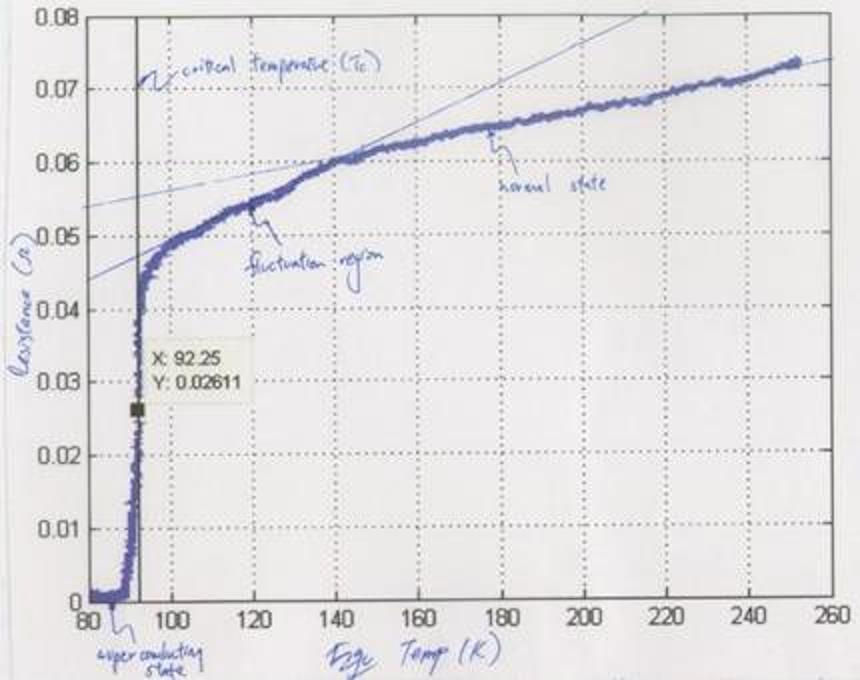
But in the second paper, there is a key plot of resistivity vs. temperature, which is what you’d hope for. Just as before, what you’d really want to see are three areas of the graph:

• above the critical temperature, a positive, non-zero resistivity that may be seen to increase (slightly) with increasing temperature,
• at the critical temperature, many data points showing the sharp decrease in resistivity from its positive, finite value all the way to zero,
• and below the critical temperature, resistivity remaining at exactly zero, with no changes or fluctuations, at all temperatures less than the critical one.

Although it’s been touted as a superconductor by Lee and Kim, the two scientists who synthesized and brought LK-99 to prominence, their own data clearly shows a non-zero resistivity to the material, even below what they claim the critical temperature is: 127 C. The fact that resistivity remains non-zero means, by definition, that this material cannot be superconducting.

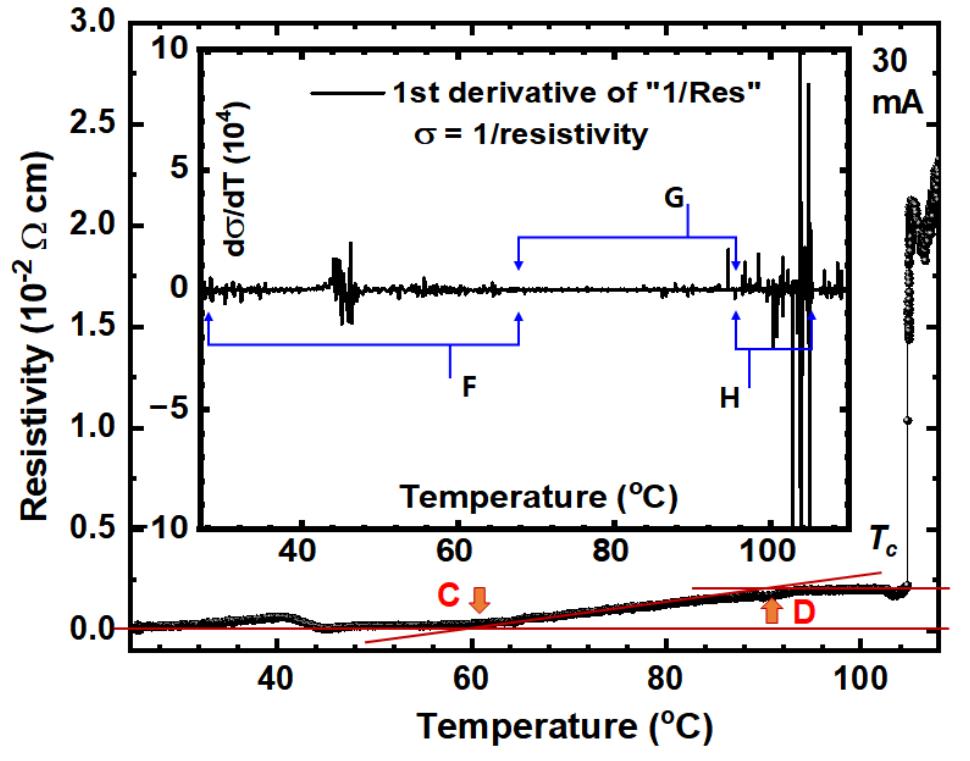
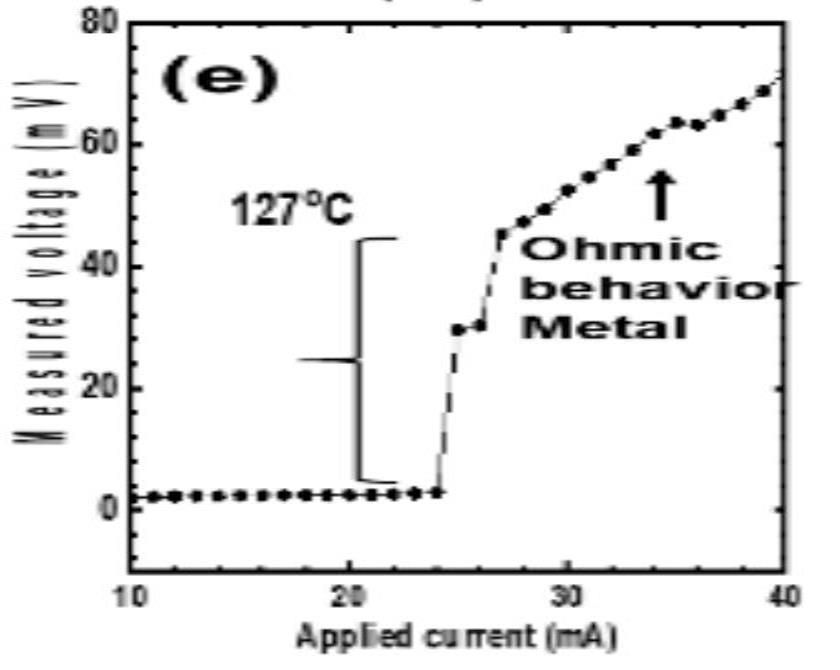
But, as you can very clearly see above, there is an abrupt drop in resistivity, but not a drop all the way to zero. In fact, the resistivity remains positive and non-zero, and then as you further decrease the temperature, it:

• first remains constant,
• then drops linearly at one rate,
• then drops linearly at a different rate,
• then dips and rapidly rises,
• and then declines once again.

Despite these changes and the clear non-constant, non-zero nature of resistivity, the authors then take the incredibly dubious step of graphing the derivative of conductivity (the inverse of resistivity) and show, with a few notable exceptions (blips in the graph), that it appears to be a constant consistent with zero.

But this is only because, over the relevant part of the graph, they’ve zoomed out so far that they aren’t properly showing that there are many different levels that are different from one another and are different from zero owing to the slopes of the resistivity differing from one another over the course of the graph. This is a deceitful presentation of the data, and a deceit that physicists in particular are especially attuned to. Any successful attempt at replication should have, as its main burden of proof, the goal of showing whether resistivity truly drops to zero (and stays there) below a critical temperature or not.

Although the authors of a July 2023 preprint paper allege that this sample is showing evidence for partial levitation due to the Meissner effect, indicating superconductivity, most Meissner effect applications wholly levitate. The fact that one side of the sample is always in contact with the magnet itself is evidence for either strong diamagnetism or weak ferromagnetism, not for superconductivity effects.

4.) Does this sample truly exhibit flux pinning as associated with the Meissner effect, or is it simply “kind of rising off of the magnet” because of either diamagnetic or ferromagnetic effects?

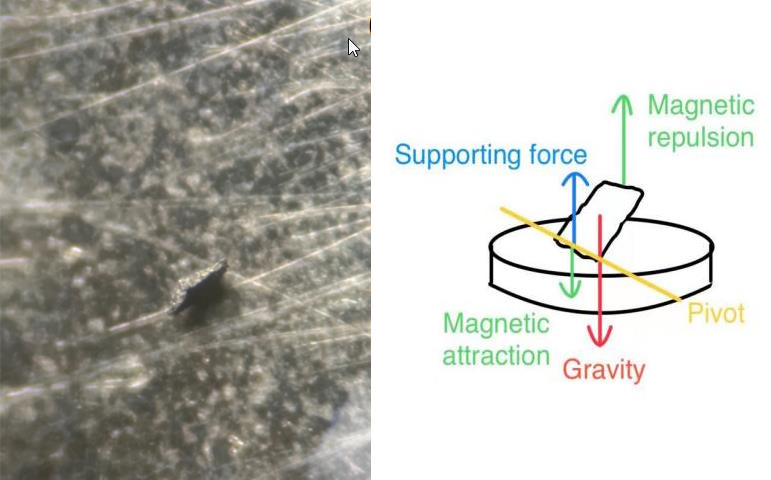
This was the whole (scientific) point of the second paper that Lee & Kim published, titled “Superconductor Pb_10−xCu_x(PO₄)₆O showing levitation at room temperature and atmospheric pressure and mechanism.” But what you see, above, is the only evidence (taken from a video that they also uploaded) for what they call magnetic levitation.

Now, it’s true that there is a magnetic levitation effect associated with (type II) superconductors: the Meissner effect. One of the hallmarks of a superconductor is that it expels all magnetic fields from inside of it. If your superconductor is pure and pristine (a type I superconductor, like a simple metal), that’s the end of the story; no magnetic fields remain inside. But if you have a type II superconductor with impurities within it, which is virtually all superconductors that are alloys, the non-uniformity of the material leads to the formation of magnetic field vortices where the impurities are.

Within each magnetic vortex, the field lines become pinned, and that’s what leads to the phenomenon of quantum magnetic levitation via the Meissner effect.

A top view and side view of a Type II superconductor exposed to a strong magnetic field. Note how the side view demonstrates where the impurities arise and the flux is pinned, while the top view displays the generated eddy currents that do not decay on account of the superconductivity.

But quantum levitation always involves phenomena that aren’t shown here, like flux pinning/quantum locking. Under quantum levitation, the entire material is always levitated; you never have one end in contact with the magnet, which is what the video and images by Lee & Kim (and team) show.

Instead, what they call “partial magnetic levitation” is an incredibly charitable interpretation of their result, and likely to be completely incorrect. Instead, what you’re more likely seeing is a simpler example of magnetism: either strong diamagnetism, which is magnetically repulsive, or an example of ferromagnetism, where you have some permanent “north-south” poles within your sample, causing one side to attract the magnet below and one side to repel it, leading to this wonky, sideways configuration you see in the Lee & Kim sample.

In the a very recent reproduction attempt, three scientists synthesized their own sample of LK-99, and reported the following:

“Using magnetization measurements on such small pieces, as well as on a large piece which does not exhibit the half levitation, we show that the samples ubiquitously contain weak yet definitive soft ferromagnetic components. We argue that, together with the pronounced shape anisotropy of the small fragments, the soft ferromagnetism is sufficient to explain the observed half levitation in strong vertical magnetic fields. Our measurements do not indicate the presence of the Meissner effect, nor zero resistance, in our samples, leading us to believe that our samples do not exhibit superconductivity.”

In a very strong and robust reproduction attempt of Lee & Kim’s LK-99 work, scientists Kaizhen Guo, Yuan Li, and Shuang Jia synthesizes several samples of LK-99 and found no evidence for superconductivity, but instead evidence for what’s known as soft ferromagnetism. Their supplemental figures, with the “partial levitation” (i.e., permanent magnet) effects shown at left and a classical explanation using standard magnetism shown at right.

One of the most dangerous things you can do, from a scientific perspective, is to ask suggestive but inconclusive questions that dance around the critical issue, rather than go straight for the critical issues themselves. When you look at unimportant clues, such as:

• a large drop in voltage at a specific current and a specific temperature,
• small measured voltages compared to earlier, large measured voltages,
• a large drop in resistance,
• and partial levitation above a permanent magnet,

it only obscures you from seeing the truth that would arise from asking the more necessary questions.

Does the voltage drop to zero and remain there? Does the resistivity truly drop to zero and remain there? Can we observe and characterize these drops in a robust fashion? Can we tell the difference between small/reduced voltage and resistivity and a value that’s truly zero? And are we observing true quantum levitation or the more common, and more mundane, phenomena of diamagnetism, paramagnetism, or ferromagnetism?

If we insisted on asking only the important questions, we’d see that we don’t have any compelling evidence at all that LK-99 is a superconductor. Until that evidence arrives, it’s most likely that we’ve simply been fooling ourselves, yet again, with wishful thinking. After all, a room temperature, ambient pressure, easily manufactured superconductor would change the world. We just don’t see the evidence that LK-99 is it.