Quantum superposition begs us to ask, “What is real?”
- In the quantum world, objects can be in multiple places at once, at least until they are measured.
- This is due to the weirdness of quantum superposition. The same experiment, repeated many times under the same conditions, can give different results.
- Analogies to understand this phenomenon all fall short. But they do beg us to ponder, “What is real?”
The world of the very, very small is a wonderland of strangeness. Molecules, atoms, and their constituent particles did not readily reveal their secrets to the scientists that wrestled with the physics of atoms in the early 20th century. Drama, frustration, anger, puzzlement, and nervous breakdowns abounded, and it is hard for us now, a full century later, to understand what was at stake. What happened was a continuous process of worldview demolition. You might have to give up believing everything you thought to be true about something. In the case of the quantum physics pioneers, that meant changing their understanding about the rules that dictate how matter behaves.
String energy
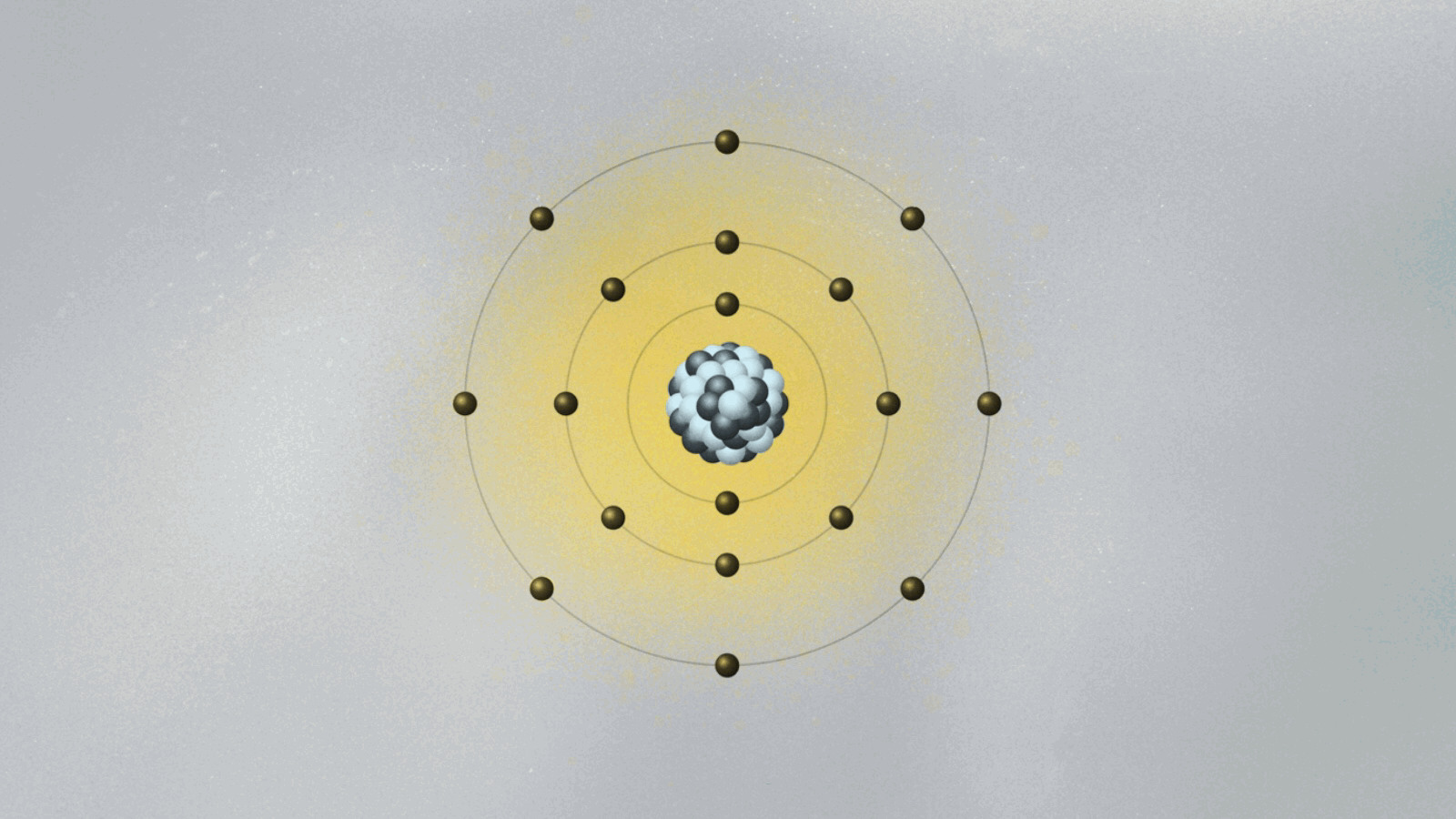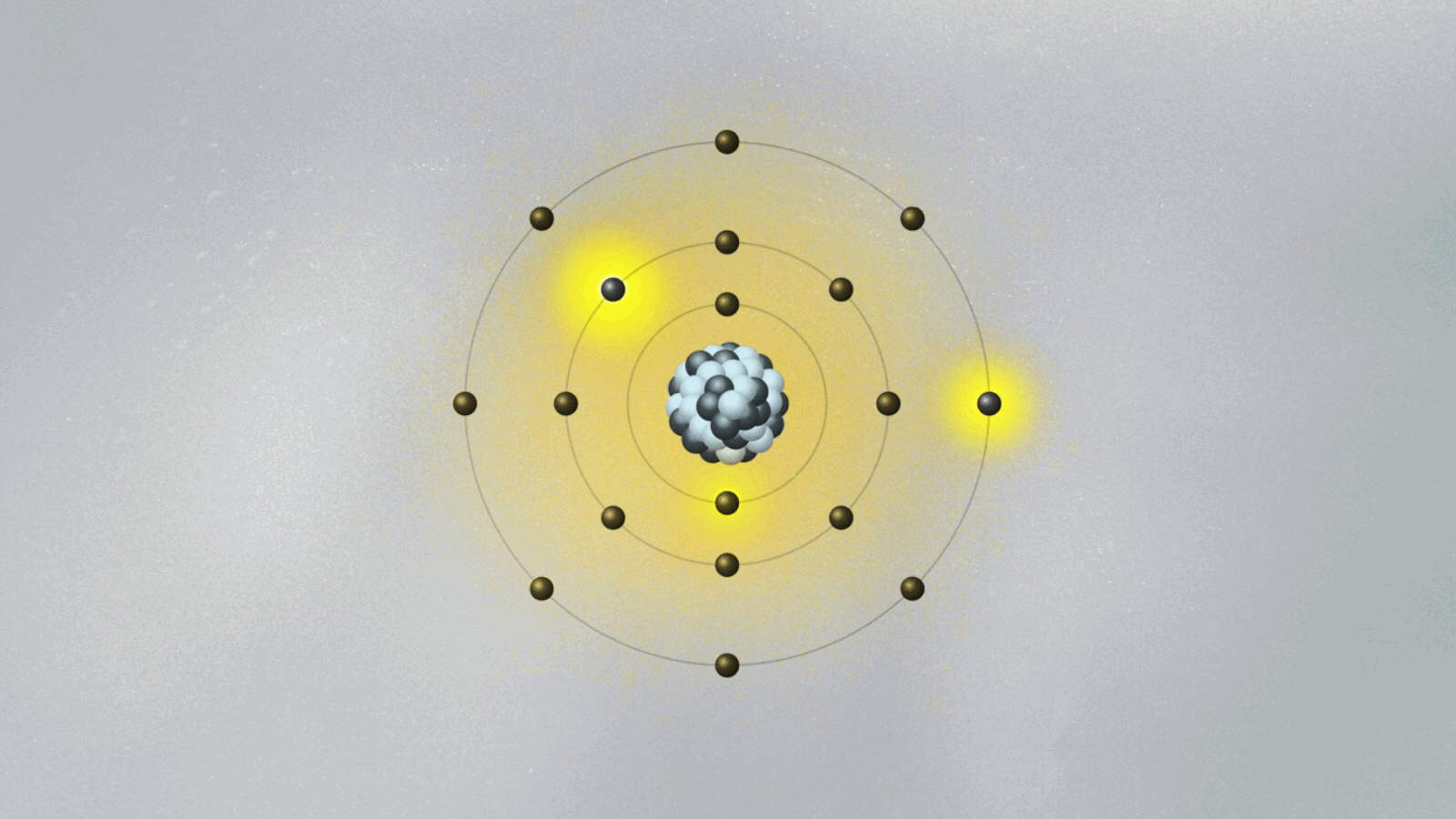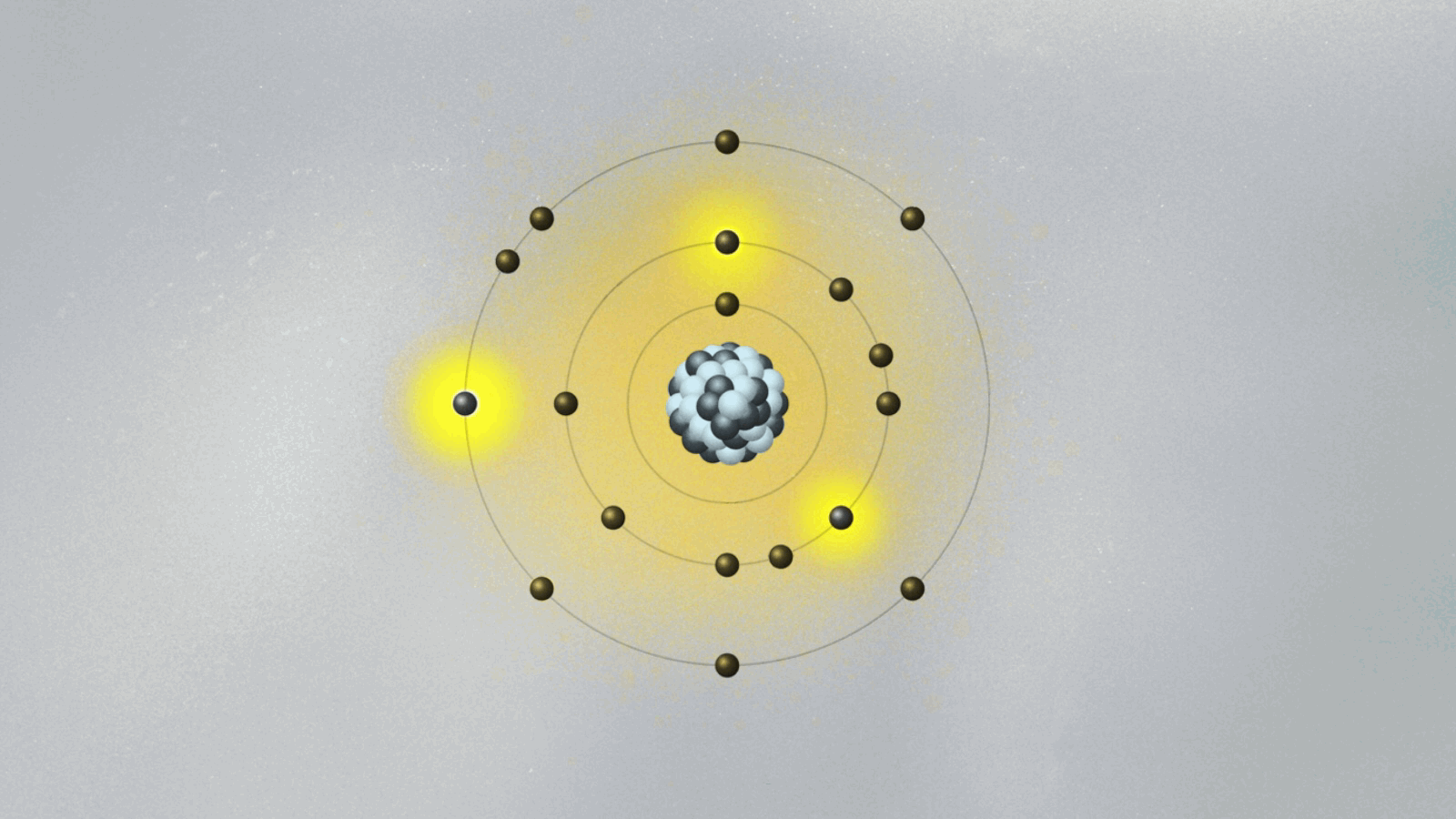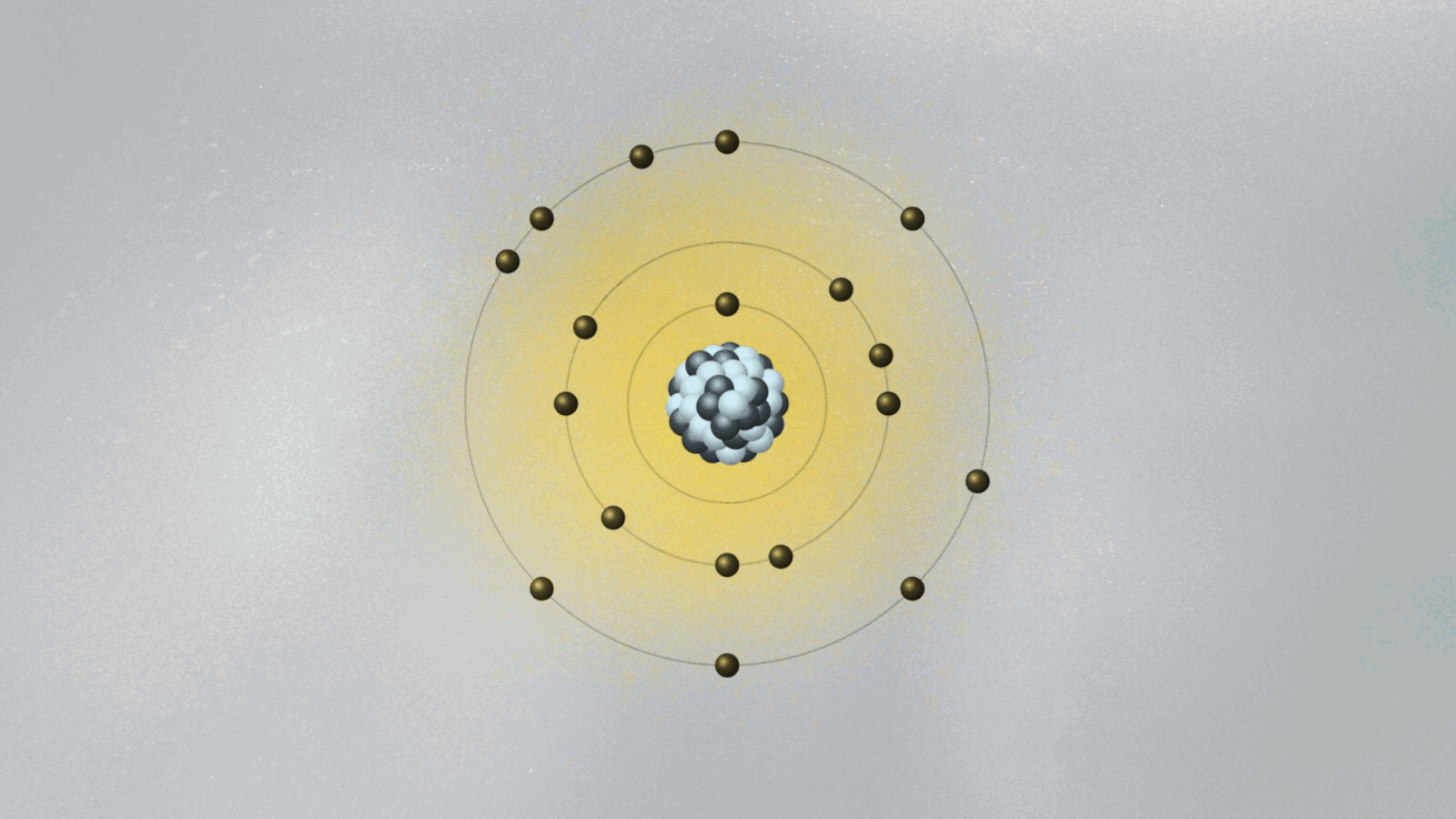
In 1913, Bohr devised a model for the atom that looked somewhat like a solar system in miniature. Electrons moved around the atomic nucleus in circular orbits. Bohr added a few twists to his model — twists that gave them a set of weird and mysterious properties. The twists were necessary for Bohr’s model to have explanatory power — that is, for it to be able to describe the results of experimental measurements. For example, electrons’ orbits were fixed like railroad tracks around the nucleus. The electron could not be in between orbits, otherwise it could fall into the nucleus. Once it got to the lowest rung in the orbital ladder, an electron stayed there unless it jumped to a higher orbit.
Clarity about why this happened started to come with de Broglie’s idea that electrons can be seen both as particles and waves. This wave-particle duality of light and matter was startling, and Heisenberg’s Uncertainty Principle gave it precision. The more precisely you localize the particle, the less precisely you know how fast it moves. Heisenberg had his own theory of quantum mechanics, a complex device to compute the possible outcomes of experiments. It was beautiful but extremely hard to calculate things with.
A little later, in 1926, Austrian physicist Erwin Schrödinger had a huge idea. What if we could write an equation for what the electron is doing around the nucleus? Since de Broglie suggested that electrons behave like waves, this would be like a wave equation. It was a truly revolutionary idea, and it reframed our understanding of quantum mechanics.
In the spirit of Maxwell’s electromagnetism, which describes light as waving electric and magnetic fields, Schrödinger pursued a wave mechanics that could describe de Broglie’s matter waves. One of the consequences of de Broglie’s idea was that if electrons were waves, then it was possible to explain why only certain orbits were allowed. To see why this is true, imagine a string being held by two people, Ana and Bob. Ana jerks it quickly, creating a wave moving toward Bob. If Bob does the same, a wave moves toward Ana. If Ana and Bob synchronize their actions, a standing wave appears, a pattern that doesn’t move left or right and that exhibits a fixed point between them called a node. If Ana and Bob move their hands faster, they will find new standing waves with two nodes, then three nodes, and so on. You can also generate standing waves by plucking a guitar string with varying strengths, until you find standing waves with different numbers of nodes. There is a one-to-one correspondence between the energy of the standing wave and the number of nodes.
The Born legacy
De Broglie pictured the electron as a standing wave around the nucleus. As such, only certain vibrating patterns would fit in a closed circle — the orbits, each characterized by a given number of nodes. The allowed orbits were identified by the number of nodes of the electron wave, each with its specific energy. Schrödinger’s wave mechanics explained why de Broglie’s picture of the electron as a standing wave was accurate. But it went much further, generalizing this simplistic picture into three spatial dimensions.
In a sequence of six remarkable papers, Schrödinger formulated his new mechanics, applied it successfully to the hydrogen atom, explained how it could be applied to produce approximate answers to more complicated situations, and proved the compatibility of his mechanics with Heisenberg’s.
The solution to Schrödinger’s equation was known as the wave function. Initially, he thought of it as describing the electron wave itself. This was in accord with classical notions of how waves evolve in time, obeying determinism. Given their initial position and velocity, we can use their equation of motion to predict what happens in the future. Schrödinger was particularly proud of this fact — that his equation restored some order to the conceptual mess caused by atomic physics. He never liked the idea of the electron “jumping” between discrete orbits.
However, Heisenberg’s Uncertainty Principle ruined this deterministic interpretation for the wave function. In the quantum world everything was fuzzy, and it was impossible to predict exactly the time evolution of the electron, be it particle or wave. The question became: Then what does this wave function mean?
Physicists were lost. How could the wave-particle duality of matter and light and Heisenberg’s Uncertainty Principle be reconciled with Schrödinger’s beautiful (and continuous) wave mechanics? Again a radical new idea was needed, and again someone had it. This time it was the turn of Max Born, who apart from being one of the principal architects of quantum mechanics was also the grandfather of 1970s rock star Olivia Newton-John.
Born proposed, correctly, that Schrödinger’s wave mechanics did not describe the evolution of the electron wave, but the probability of finding the electron in this or that position in space. Solving Schrödinger’s equation, physicists compute how this probability evolves in time. We cannot predict with any certainty whether the electron will be found here or there. We can only give probabilities of it being found here or there once a measurement is made. In quantum mechanics, the probability evolves deterministically according to the wave equation, but the electron itself does not. The same experiment, repeated many times under the same conditions, can give different results.
Quantum superposition
This is quite strange. For the first time, physics has an equation that does not describe the behavior of something physical belonging to an object — like the position, momentum, or energy of a ball or planet. The wave function is not something real in the world. (At least, it is not so to this physicist. We will address this cumbersome issue soon.) Its square — actually, its absolute value, since it is a complex quantity — gives the probability of finding the particle at a certain point in space once a measurement is made. But what happens before the measurement? We can’t tell. What we say is that the wave function is a superposition of many possible states for the electron. Each state represents a position the electron might be found at once a measurement is made.
A possibly useful image (they are all iffy) is to picture yourself in a room that is totally dark, walking toward a wall where many pictures are hanging. Lights turn on when you reach a specific location on the wall, in front of a painting. Of course, you know that you are a single person walking toward one of the paintings. But if you were a subatomic particle like an electron or a photon, there would be many copies of you walking toward the wall simultaneously. You would be in a superposition of many yous, and only one copy would reach the wall and cause the lights to turn on. Each copy of you would have a different probability of reaching the wall. Repeating the experiment many times, these different probabilities are uncovered.
Are all copies moving in the dark room real, or only the one that hits the wall and turns on the lights? If only that one is real, how come others could also have hit the wall? This effect, known as quantum superposition, is perhaps the weirdest of them all. So weird and fascinating that it deserves a whole article.