The Surprising Reason Why Neutron Stars Don’t All Collapse To Form Black Holes

There’s something very special inside a proton and neutron that holds the key.
There are few things in the Universe that are as easy to form, in theory, as black holes are. Bring enough mass into a compact volume and it gets more and more difficult to gravitationally escape from it. If you were to gather enough matter in a single spot and let gravitation do its thing, you’d eventually pass a critical threshold, where the speed you’d need to gravitationally escape would exceed the speed of light. Reach that point, and you’ll create a black hole.
But real, normal matter will very much resist getting there. Hydrogen, the most common element in the Universe, will fuse in a chain reaction at high temperatures and densities to create a star, rather than a black hole. Burned out stellar cores, like white dwarfs and neutron stars, can also resist gravitational collapse and stave off becoming a black hole. But while white dwarfs can reach only 1.4 times the mass of the Sun, neutron stars can get twice as massive. At long last, we finally understand why.

In our Universe, the matter-based objects we know of are all made of just a few simple ingredients: protons, neutrons, and electrons. Each proton and neutron is made up of three quarks, with a proton containing two up and one down quark, and a neutron containing one up and two downs. On the other hand, electrons themselves are fundamental particles. Although particles come in two classes — fermions and bosons — both quarks and electrons are fermions.
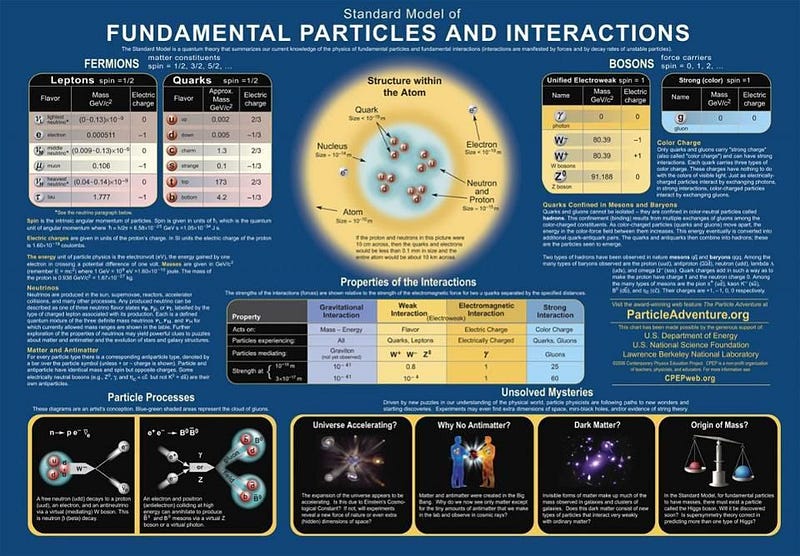
Why should you care? It turns out that these classification properties are vitally important when it comes to the question of black hole formation. Fermions have a few properties that bosons don’t, including:
- they have half-integer (e.g., ±1/2, ±3/2, ±5/2, etc.) spins as opposed to integer (0, ±1, ±2, etc.) spins,
- they have antiparticle counterparts; there are no anti-bosons,
- and they obey the Pauli Exclusion Principle, whereas bosons don’t.
That last property is the key to staving off collapse into a black hole.
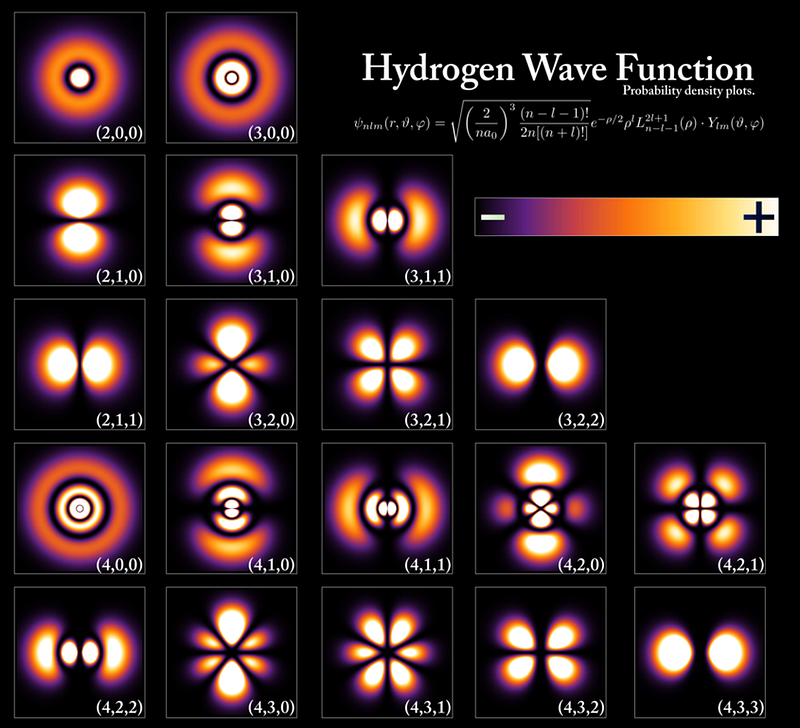
The Pauli exclusion principle, which only applies to fermions, not bosons, states, explicitly, that in any quantum system, no two fermions can occupy the same quantum state. It means that if you take, say, an electron and put it in a particular location, it will have a set of properties in that state: energy levels, angular momentum, etc.
If you take a second electron and add it to your system, however, in the same location, it is forbidden from having those same quantum numbers. It must either occupy a different energy level, have a different spin (+1/2 if the first was -1/2, for example), or occupy a different location in space. This principle explains why the periodic table is arranged as it is.
This is why atoms have different properties, why they bind together in the intricate combinations that they do, and why each element in the periodic table is unique: because the electron configuration of each type of atom is unlike any other.
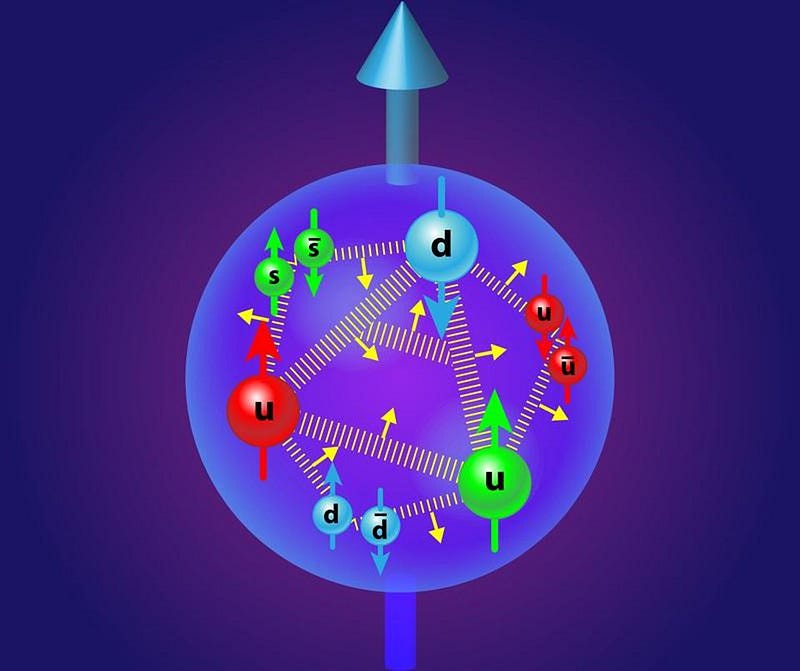
Protons and neutrons are similar. Despite being composite particles, made up of three quarks apiece, they behave as single, individual fermions themselves. They, too, obey the Pauli Exclusion Principle, and no two protons or neutrons can occupy the same quantum state. The fact that electrons are fermions is what keeps white dwarf stars from collapsing under their own gravity; the fact that neutrons are fermions prevents neutron stars from collapsing further. The Pauli exclusion principle responsible for atomic structure is responsible for keeping the densest physical objects of all from becoming black holes.

And yet, when you look at the white dwarf stars we have in the Universe, they cap out at around 1.4 solar masses: the Chandrasekhar mass limit. The quantum degeneracy pressure arising from the fact that no two electrons can occupy the same quantum state is what prevents black holes from forming until that threshold is crossed.
In neutron stars, there should be a similar mass limit: the Tolman-Oppenheimer-Volkoff limit. Initially, it was anticipated that this would be about the same as the Chandrasekhar mass limit, since the underlying physics is the same. Sure, it’s not specifically electrons that are providing the quantum degeneracy pressure, but the principle (and the equations) are pretty much the same. But we now know, from our observations, that there are neutron stars much more massive than 1.4 solar masses, perhaps rising as high as 2.3 or 2.5 times the mass of our Sun.

And yet, there are reasons for the differences. In neutron stars, the strong nuclear force plays a role, causing a larger effective repulsion than for a simple model of degenerate, cold gases of fermions (which is what’s relevant for electrons). For the past 20+ years, calculations of the theoretical mass limit for neutron stars have varied tremendously: from about 1.5 to 3.0 solar masses. The reason for the uncertainty has been the unknowns surrounding the behavior of extremely dense matter, like the densities you’ll find inside an atomic nucleus, are not well known.
Or rather, these unknowns plagued us for a long time, until a new paper last month changed all of that. With the publication of their new paper in Nature, The pressure distribution inside the proton, coauthors V. D. Burkert, L. Elouadrhiri, and F. X. Girod may have just achieved the key advance needed to understand what’s happening inside neutron stars.
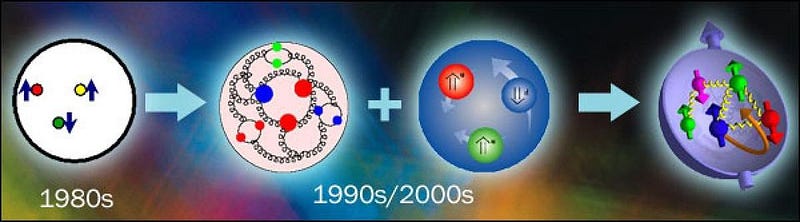
Our models of nucleons like protons and neutrons have improved tremendously over the past few decades, coincident with improvements in both computational and experimental techniques. The latest research uses an old technique known as Compton scattering, where electrons are fired at the internal structure of a proton to probe its structure. When an electron interacts (electromagnetically) with a quark, it emits a high-energy photon, along with a scattered electron and leads to nuclear recoil. By measuring all three products, you can calculate the pressure distribution experienced by the quarks inside the atomic nucleus. In a shocking find, the average peak pressure, near the center of the proton, comes out to 10³⁵ pascals: a greater pressure than neutron stars experience anywhere.
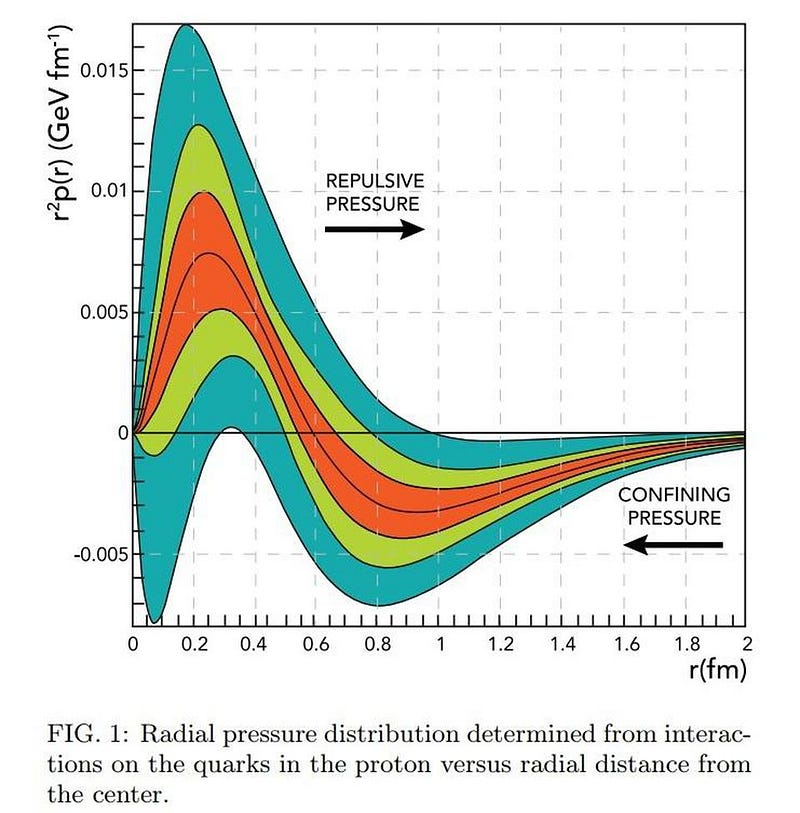
In other words, by understanding how the pressure distribution inside an individual nucleon works, we can calculate when and under what conditions that pressure can be overcome. Although the experiment was only done for protons, the results should be analogous for neutrons, too, meaning that, in the future, we should be able to calculate a more exact limit for the masses of neutron stars.
The measurements of the enormous pressure inside the proton, as well as the distribution of that pressure, show us what’s responsible for preventing the collapse of neutron stars. It’s the internal pressure inside each proton and neutron, arising from the strong force, that holds up neutron stars when white dwarfs have long given out. Determining exactly where that mass threshold is just got a great boost. Rather than solely relying on astrophysical observations, the experimental side of nuclear physics may provide the guidepost we need to theoretically understand where the limits of neutron stars actually lie.
Ethan Siegel is the author of Beyond the Galaxy and Treknology. You can pre-order his third book, currently in development: the Encyclopaedia Cosmologica.