No, Quantum Tunneling Didn’t Break The Speed Of Light; Nothing Does


If you don’t look at the whole picture, it’s all too easy to fool yourself.
If you throw a tennis ball at a solid wall, it will strike the wall and ricochet back at you 100% of the time, just like you’d expect. In physics, a sufficiently strong barrier will prevent any incoming object from passing through it. But at the quantum level, this isn’t strictly true. If you replace a tennis ball with a quantum particle and a solid wall with any quantum mechanical barrier, there’s a finite probability that the particle will actually tunnel through the barrier, where it winds up being detected on the other side. It’s as though you threw the tennis ball at the wall and it went right through, unimpeded by the wall at all.
Scientists have, for the first time, successfully measured how long the tunneling process takes, and found that it was instantaneous. But this doesn’t mean it happened faster than the speed of light. Nothing breaks that speed, and here’s how you can see it for yourself.
When you think of the quantum Universe, chances are you think of tiny, individual particles all zipping around and colliding into one another. But one of the counterintuitive aspects of the quantum nature of reality is that this picture doesn’t quite explain what we observe. We know that there’s a fundamental uncertainty inherent to certain properties (like the positions) of quantum particles, and we can only describe them fully by using probability.
What this means is that if you take a single quantum particle, place it down at any one location, and ask “where is it now?” at some later time, you won’t find it simply by multiplying its speed by the amount of time that’s passed. The quantum nature of this particle means that its position is defined by a wavefunction, and that’s not well-determined. We can only give you the probabilities of where you might find it.
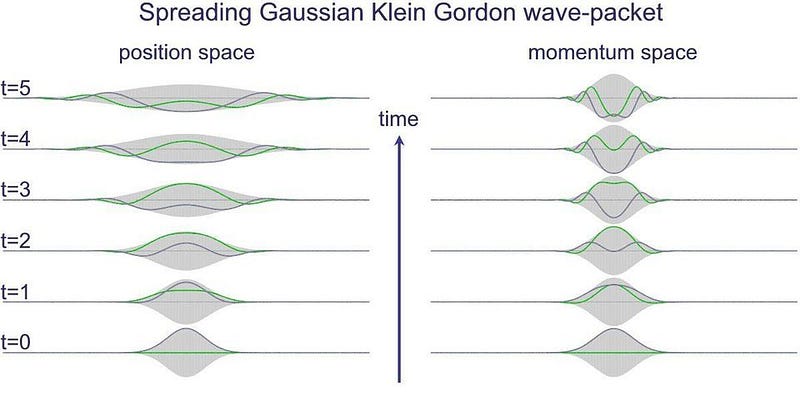
This bizarre, counterintuitive property of quantum physics isn’t a limitation of our measurement equipment, but rather is a fundamental property of our reality and the rules that govern it. Whether you’re talking about:
- a particle at rest,
- a free particle traveling through space,
- a bound particle (like an electron in an atom) that’s restricted as far as where it’s allowed to be,
- or a particle that encounters an obstacle that restricts what quantum states it’s allowed to occupy,
there are no certainties until you make a measurement, only probabilities.
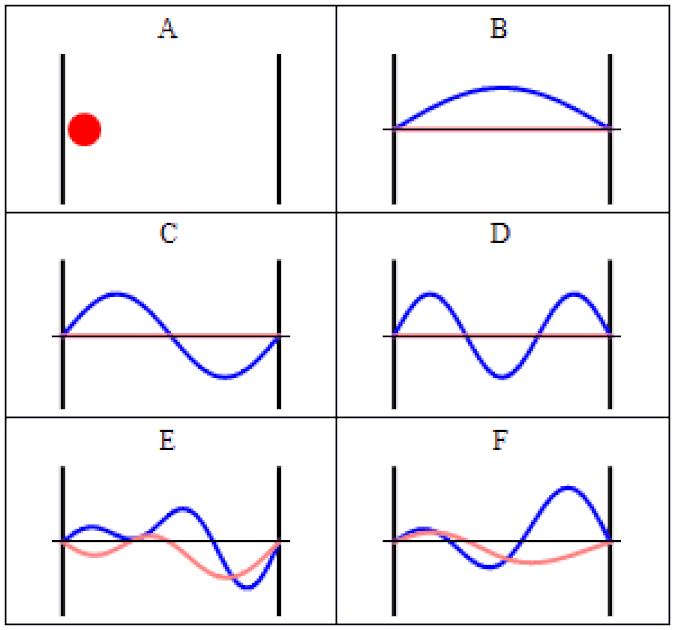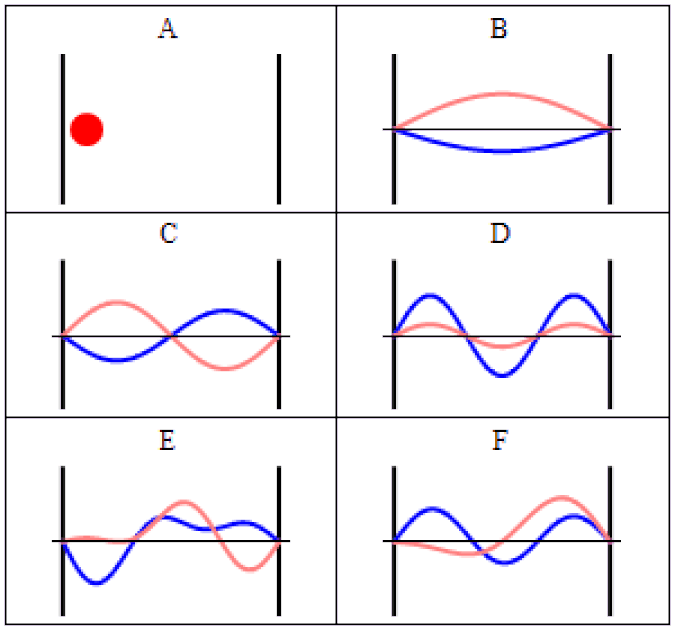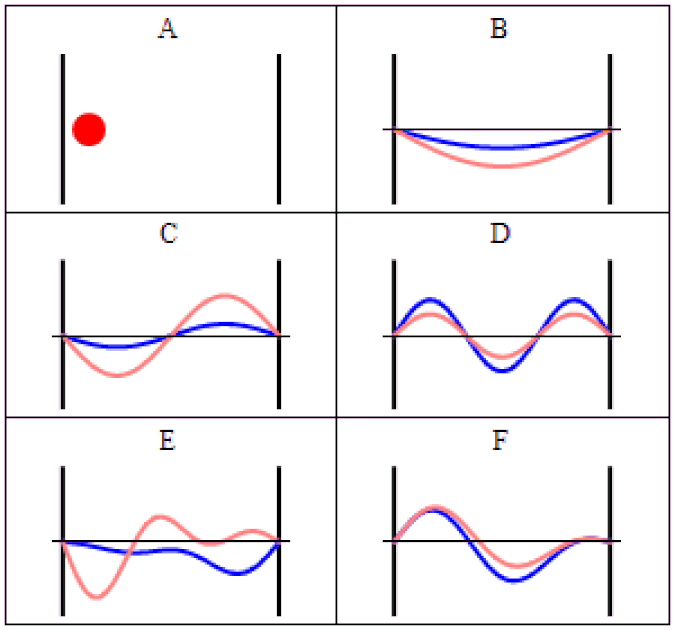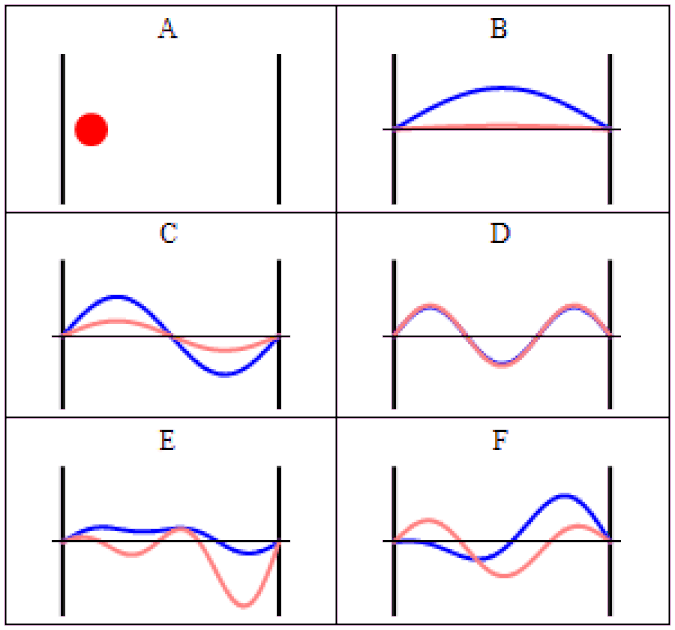
So you might think, if you have a system that has a probability of tunneling from one side of a quantum barrier (like bound in an atom, or in a false minimum) to the other, there would be a restriction on how quickly that transition could occur. Maybe it would depend on the size of the barrier, the thickness of the barrier, or some other factor that was related to its physical properties. After all, in this Universe, everything should be limited by the speed of light.
The simplest setup of all is to take one single particle, like an electron, bound in a restricted system, like a hydrogen atom. There’s a finite, non-zero probability that it will tunnel to an unbound state. By imaging it with the proper equipment — ultra-fast photons, for instance — you can accurately measure the time interval it takes to tunnel from a bound to an unbound state.

Researchers at the Australian Attosecond Science Facility have done exactly that, finding that this simplest of transitions takes at most 1.8 attoseconds (1.8 × 10^-18 s). That means, at the speed of light, we’re talking about traveling a distance of just 5.4 ångströms. According to Robert Sang, one of the lead researchers:
There’s a well-defined point where we can start that interaction, and there’s a point where we know where that electron should come out [the interaction itself is] instantaneous. So anything that varies from that time we know that it’s taken that long to go through the barrier… It came out to agree with the theory within experimental uncertainty being consistent with instantaneous tunneling.
While this has fascinating implications for the practical applications of, say, the construction of a quantum-limited transistor, “instantaneous” in this context doesn’t mean that it violates Einstein’s relativity.
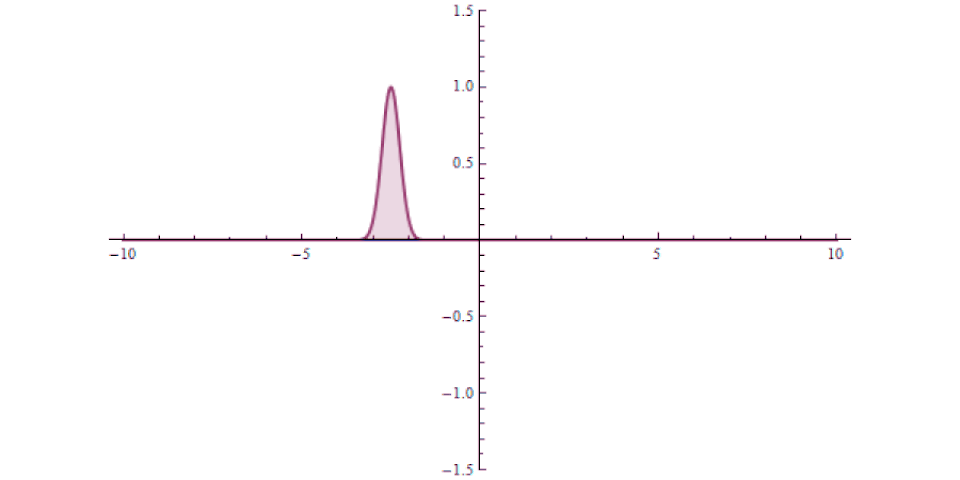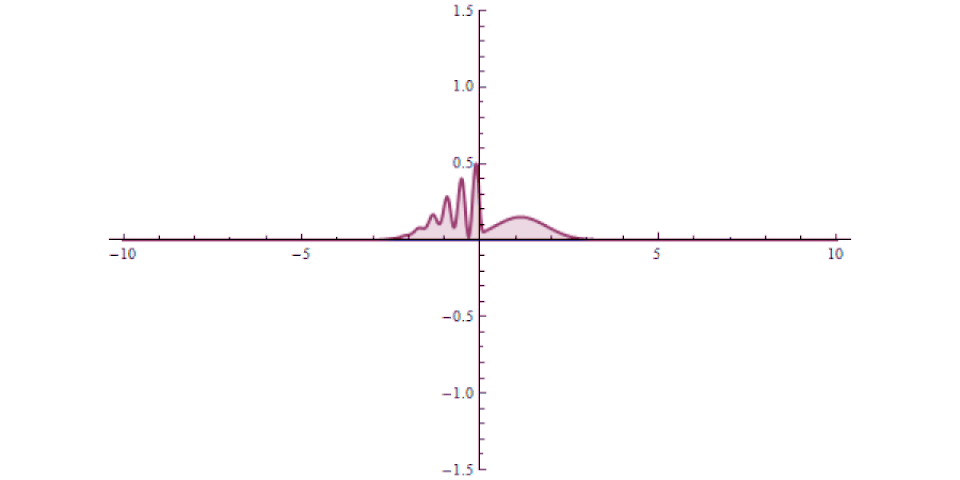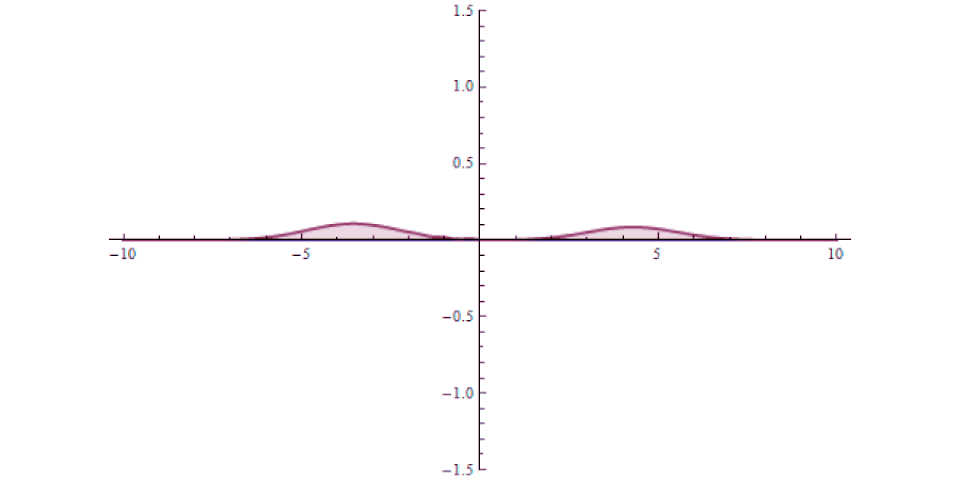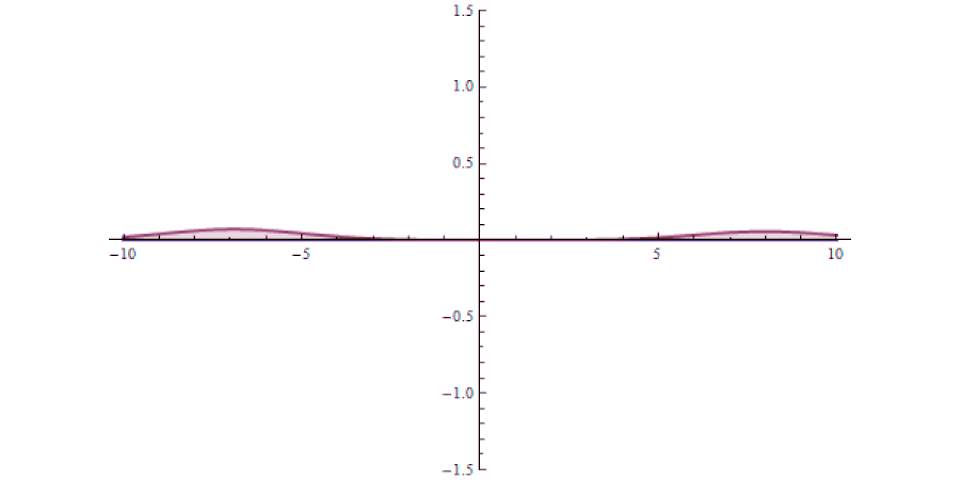
It isn’t as though at one instant you can say “this particle is over there” and then, some tiny amount of time later, you can say “this particle is now located here instead” with that change-in-distance divided by the change-in-time exceeding the speed of light. The experiment, which is remarkable for how precise and clean it was in only involving a single particle in a single, bound system, simply shows that there’s no fundamental quantum delay in this tunneling transition.
But it also helps expose how physicists have managed to exploit a many-particle system in order to create the illusion of something traveling faster than light: a result which gets misreported every few years in the popular media. Imagine you’ve got a set of quantum particles, bunched together into a tight pulse, tunneling or otherwise traveling through a barrier of some sort.

It’s truly remarkable at how successful we’ve become at imaging pulses that move at speeds that approach or even equal the speed of light, thanks to novel techniques and technologies. What you can do is measure:
- where this pulse is located in space at a certain instant in time, before it encounters a barrier,
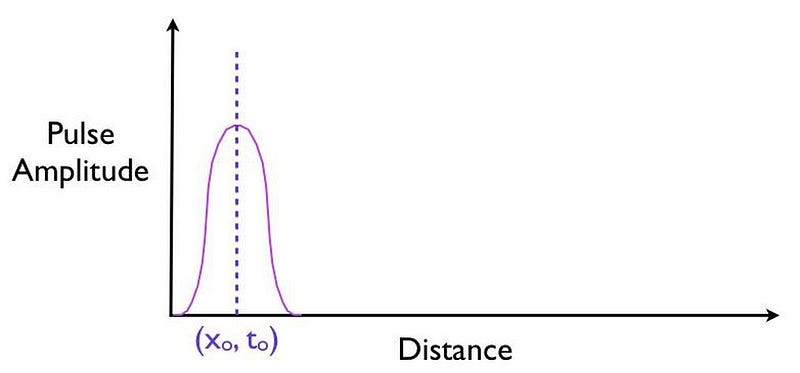
- where and when you expect that pulse to arrive if it were to move at the speed of light and successfully tunnel through the barrier,
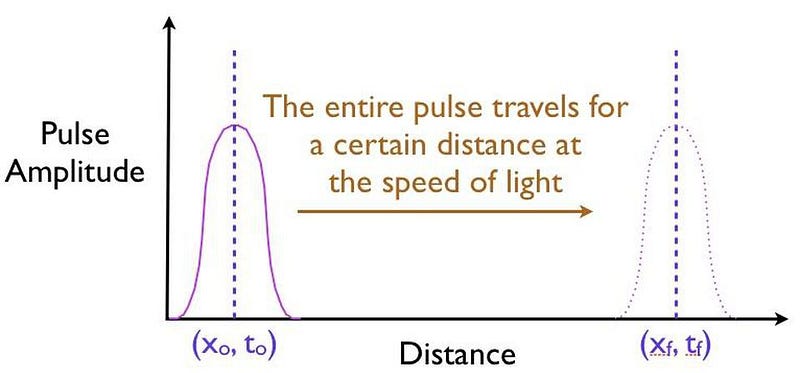
- and then comparing your measurement for where the pulse is located in space at a later instant in time, after successfully tunneling through the barrier.
It might surprise you to learn that the pulse that you detect on the other side of the barrier can easily be found appearing to move faster than the speed of light would seem to permit!

You might think, based on what you just read about the speed of quantum tunneling being instantaneous, that this means that particles can travel infinitely fast, breaking the speed of light, through a quantum mechanical barrier of finite, non-zero thickness. That’s the misinterpretation that always crops up, and how people fool themselves (and unscrupulous news organizations try to fool you) into thinking they’re breaking the speed of light.
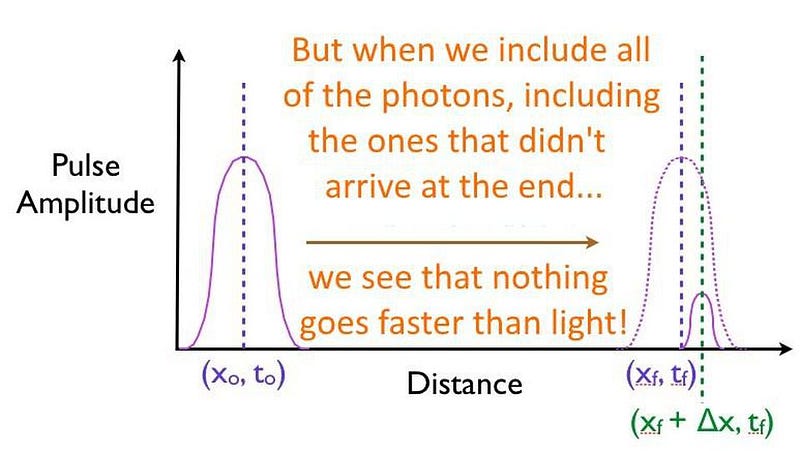
But all that’s happening here is a portion of the quantum particles found in the pulse tunnels through the barrier, while the majority of the particles does what tennis balls do: they bounce back, failing to arrive at the destination. If you can front-load which particles make it through the barrier, preferentially cutting off the particles in the back of the pulse, you’ll falsely measure a faster-than-light speed, even though no individual particle actually breaks the speed of light.
So what does this new result actually mean, then?
Simply that the actual process of tunneling itself, where the transition occurs from being in a bound state on one side of a quantum barrier to an unbound sate on the other side, doesn’t take any extra, additional time on top of all the other physical effects. Moving a certain distance in a given time is still limited by Einstein’s relativity, though, with this restriction applying to each and every particle under all circumstances. It’s an incredible feat that scientists have made this measurement directly, for a single particle, and demonstrated that there is no delay inherent to the tunneling process itself.
But going faster than light? That’s still restricted to the realm of science fiction alone.
Ethan Siegel is the author of Beyond the Galaxy and Treknology. You can pre-order his third book, currently in development: the Encyclopaedia Cosmologica.