Does mass increase when nearing the speed of light?

- When objects approach the speed of light, conventional rules about force, mass, and acceleration no longer apply. We have to use a relativistic version instead.
- While modern approaches normally talk about time dilation and length contraction, the earliest formulations instead dealt with a new concept: relativistic mass.
- Is it really true that objects become more and more massive as you approach the speed of light? It's a problematic way to think about it, and even Einstein fell for this mistake.
No matter who you are, where you are, or how quickly you’re moving, the laws of physics will appear exactly the same to you as they will to any other observer in the Universe. This concept — that the laws of physics don’t change as you move from one location to another or one moment to the next — is known as the principle of relativity, and it goes all the way back not to Einstein, but even farther: to at least the time of Galileo. If you exert a force on an object, it will accelerate (i.e., change its momentum), and the amount of its acceleration is directly related to the force on the object divided by its mass. In terms of an equation, this is Newton’s famous F = ma: force equals mass times acceleration.
But when we discovered particles that moved close to the speed of light, suddenly a contradiction emerged. If you exert too large of a force on a small mass, and forces cause acceleration, then it should be possible to accelerate a massive object to reach or even exceed the speed of light! This isn’t possible, of course, and it was Einstein’s relativity that gave us a way out. It was commonly explained by what we call “relativistic mass,” or the notion that as you got closer to the speed of light, the mass of an object increased, so the same force would cause a smaller acceleration, preventing you from ever reaching the speed of light. But is this “relativistic mass” interpretation correct? Only kind of. Here’s the science of why.

The first thing it’s vital to understand is that the principle of relativity, no matter how quickly you’re moving or where you’re located, is still always true: the laws of physics really are the same for everyone, regardless of where you’re located or when you’re making that measurement. The thing that Einstein knew (that both Newton and Galileo had no way of knowing) was this: the speed of light in a vacuum must be exactly the same for everyone. This is a tremendous realization that runs counter to our intuition about the world.
Imagine you’ve got a car that can travel at 100 kilometers per hour (62 mph). Imagine, attached to that car, you’ve got a cannon that can accelerate a cannonball from rest to that exact same speed: 100 kilometers per hour (62 miles per hour). Now, imagine your car is moving and you fire that cannonball, but you can control which way the cannon is pointed.
- If you point the cannon in the same direction that the car is moving, the cannonball will move at 200 kph (124 mph): the car’s speed plus the cannonball’s speed.
- If you point the cannon upward while the car moves forward, the cannonball will move at 141 kph (88 mph): a combination of forward and upward, at a 45 degree angle.
- And if you point the cannon in reverse, firing the cannonball backward while the car moves forward, the cannonball will come out at 0 kph (0 mph): the two speeds will exactly cancel each other out.

This is what we commonly experience and also lines up with what we expect. And this is also experimentally true, at least, for the non-relativistic world. But if we replaced that cannon with a flashlight instead, the story would be very different. You can take a car, a train, a plane, or a rocket, traveling at whatever speed you like, and shine a flashlight from it in any direction you like.
That flashlight will emit photons at the speed of light, or 299,792,458 m/s, and those photons will always travel at that same exact speed.
- You can fire the photons in the same direction your vehicle is moving, and they’ll still move at 299,792,458 m/s.
- You can fire the photons at an angle to the direction that you’re moving, and while this might change the direction-of-motion of the photons, they’ll still move at that same speed: 299,792,458 m/s.
- And you can fire the photons directly reversed to your direction of motion, and still, they’ll travel at 299,792,458 m/s.
That speed that the photons travel at will be the same as ever, the speed of light, not only from your perspective, but from the perspective of anyone looking on. The only difference that anyone will see, dependent on how fast both you (the emitter) and they (the observer) are moving, is in the wavelength of that light: redder (longer-wavelength) if you’re mutually moving away from each other, bluer (shorter-wavelength) if you’re moving mutually toward each other.
This was the key realization that Einstein had when he was devising his original theory of Special Relativity. He tried to imagine what light — which he knew to be an electromagnetic wave — would look like to someone who was following that wave at speeds that were close to the speed of light.
Although we don’t often think of it in these terms, the fact that light is an electromagnetic wave means:
- that this light wave carries energy,
- that it creates electric and magnetic fields as it propagates through space,
- those fields oscillate, in phase, and at 90-degree angles to one another,
- and when they pass by other charged particles, like electrons, they can cause them to periodically move, because charged particles experience forces (and hence, accelerations) when they’re subjected to electric and/or magnetic fields.
This was cemented in the 1860s and 1870s, in the aftermath of the work of James Clerk Maxwell, whose equations are still sufficient to govern the entirety of classical electromagnetism. You use this technology daily: every time an antenna “picks up” a signal, that signal arises from the charged particles in that antenna moving in response to those electromagnetic waves.
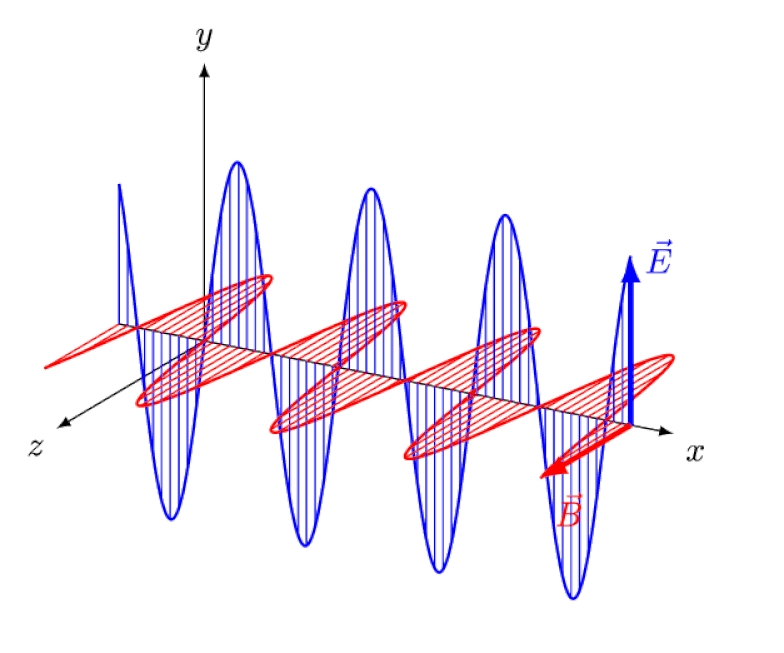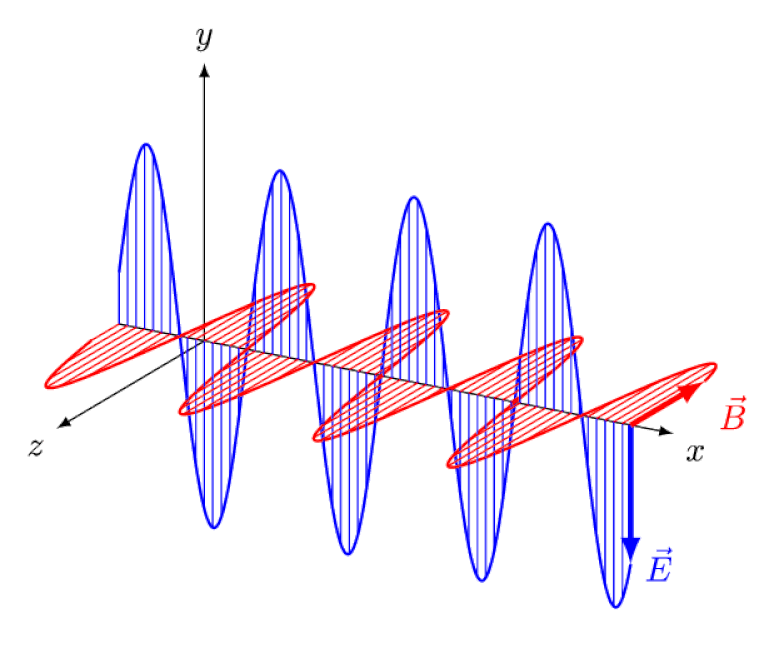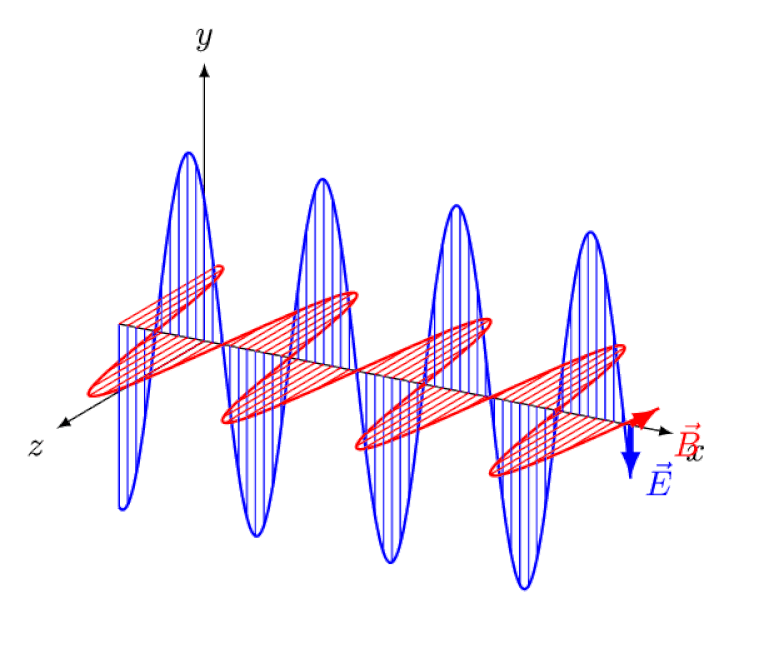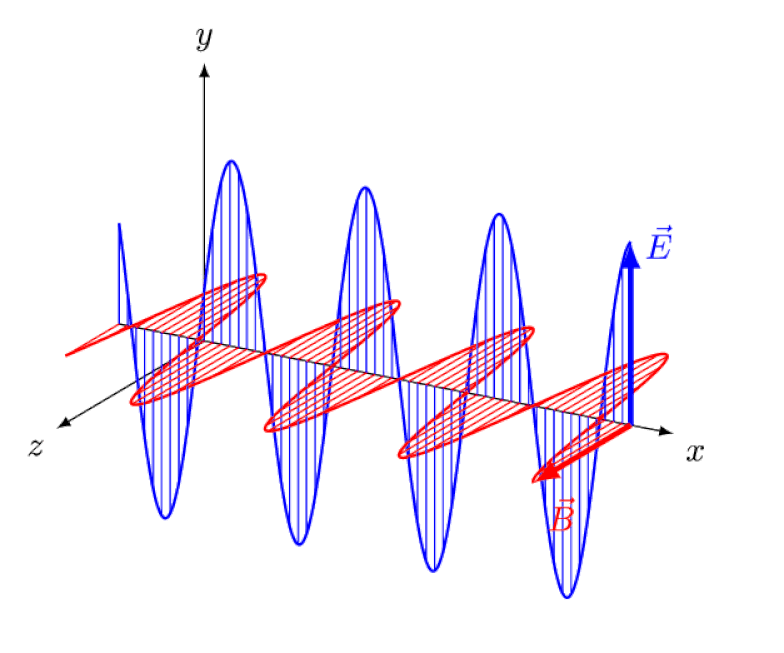
Einstein tried to think of what it would be like to follow this wave from behind, with an observer watching electric and magnetic fields oscillate in front of them. But, of course, this never occurs. No matter who you are, where you are, when you are, or how quickly you’re moving, you — and everyone else — always sees light move at exactly the same speed: the speed of light.
But not everything about light is the same for all observers. The fact that the observed wavelength of light changes dependent on how the source and the observer are moving relative to one another means that a few other things about light must change as well.
- The frequency of light must change, because frequency multiplied by wavelength always equals the speed of light, which is a constant.
- The energy of each quantum of light must change, because the energy of each photon equals Planck’s constant (which is a constant) multiplied by frequency.
- And the momentum of each quantum of light must change as well, because momentum (for light) equals the energy divided by the speed of light.
This last part is critical for our understanding, because momentum is the key link between our old school, classical, Galilean-and-Newtonian way of thinking and our new, relativistically invariant way of thinking that came along with Einstein.

Light, remember, ranges in energy tremendously, from gamma ray photons at the highest energies down through X-rays, ultraviolet light, visible light (from violet to blue to green to yellow to orange to red), infrared light, microwave light, and finally radio light at the lowest energies. The higher your energy-per-photon, the shorter your wavelength, the higher your frequency, and the greater the amount of momentum that you carry; the lower your energy-per-photon, the longer your wavelength, the lower your frequency, and the smaller your momentum is.
Light can also, as Einstein himself demonstrated with his 1905 research into the photoelectric effect, transfer energy and momentum into matter: massive particles. If the only law we had was Newton’s law the way we’re used to seeing it — as force equals mass times acceleration (F = ma) — light would be in trouble. With no mass inherent to photons, this equation wouldn’t make any sense. But Newton himself didn’t write “F = ma” like we often suppose, but rather that “force is the time rate of change of momentum,” or that applying a force causes a “change in momentum” over time.

So, what does that mean momentum is? Although many physicists have their own definition, the one I’ve always liked is, “It’s a measure of the quantity of your motion.” If you imagine a dockyard, you can imagine running a number of things into that dock.
- A dinghy might be able to move either relatively slowly or quickly, but with its low mass, its momentum will remain low. The force it exerts on the dock, when it collides, will be limited, and only the weakest docks will suffer any structural damage if hit by a dinghy.
- Someone who fires a firearm at that dock, however, is going to experience something different. Even though the projectiles — whether bullets, cannonballs, or something more damaging like artillery shells — may be low in mass, they’ll be moving at very high (but still non-relativistic) speeds. With 0.01% the mass but 10000% the velocity of a dinghy, their momenta can be just as high, but the force will be spread over a much smaller area. The structural damage will be significant, but only in very localized places.
- Or you could run an extremely slow-moving but massive object, like a cruise ship, a superyacht, or a battleship, into that dock at an extremely low speed. With millions of times the mass of a dinghy — they can weigh tens of thousands of tonnes — even a tiny speed can result in a completely destroyed dock. Momentum, for high-mass objects, doesn’t mess around.

The problem is, going all the way back to Newton, that the force you exert on something is equal to a change in momentum over time. If you exert a force on an object for a certain duration, it’s going to change that object’s momentum by a specific amount. This change doesn’t depend on how fast an object is moving alone, but only by the “quantity of motion” it possesses: its momentum.
So what is it, then, that happens to an object’s momentum when it gets close to the speed of light? That’s really what we’re trying to understand when we talk about force, momentum, acceleration, and velocity when we near the speed of light. If an object is moving at 50% the speed of light and it has a cannon that’s capable of firing a projectile at 50% the speed of light, what will happen when both speeds point in the same direction?
You know you can’t reach the speed of light for a massive object, so the naive thought that “50% the speed of light + 50% the speed of light = 100% the speed of light” has to be wrong. But the force on that cannonball is going to change its momentum by exactly the same amount when fired from a relativistically-moving frame-of-reference as it will when fired from rest. If firing the cannonball from rest changes its momentum by a certain amount, leaving it with a speed that’s 50% the speed of light, then firing it from a perspective where it’s already moving at 50% the speed of light must change its momentum by that same amount. Why, then, wouldn’t its speed be 100% the speed of light?

Understanding the answer is the key to understanding relativity: it’s because the “classical” formula for momentum — that momentum equals mass multiplied by velocity — is only a non-relativistic approximation. In reality, you have to use the formula for relativistic momentum, which is a little bit different, and involves a factor that physicists call gamma (γ): the Lorentz factor, which increases the closer you move to the speed of light. For a fast-moving particle, momentum isn’t just mass multiplied by velocity, but mass multiplied by velocity multiplied by gamma.
Applying the same force that you applied to an object at rest to an object in motion, even in relativistic motion, will still change its momentum by the same amount, but all of that momentum won’t go into increasing its velocity; some of it will go into increasing the value of gamma, the Lorentz factor. For the earlier example, a rocket moving at 50% the speed of light that fires a cannonball at 50% the speed of light will result in a cannonball traveling at 80% the speed of light, with a Lorentz factor of 1.6667 along for the ride. The idea of “relativistic mass” is very old and was popularized by Arthur Eddington, the astronomer whose 1919 solar eclipse expedition validated Einstein’s theory of General Relativity, but it takes a certain liberty: it assumes that the Lorentz factor (γ) and the rest mass (m) get multiplied together, an assumption that no physical measurement or observation can test for.
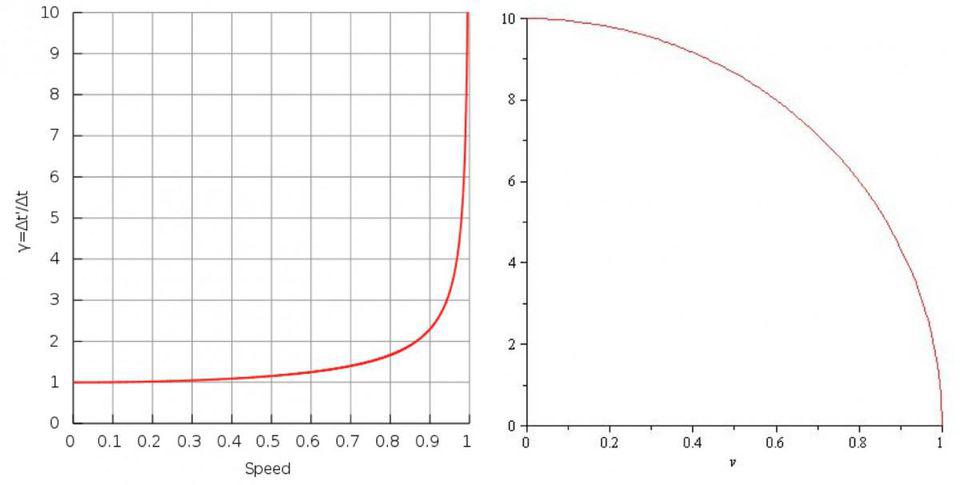
The whole point of going through all of this is to understand that when you move close to the speed of light, there are many important quantities that no longer obey our classical equations. You can’t just add velocities together the way Galileo or Newton did; you have to add them relativistically.
You can’t just treat distances as fixed and absolute; you have to understand that they contract along the direction of motion. And you can’t even treat time as though it passes the same for you as it does for someone else; the passage of time is relative, and dilates for observers moving at different relative velocities.

It’s tempting, but ultimately incorrect, to blame the mismatch between the classical world and the relativistic world on the idea of relativistic mass. For massive particles that move close to the speed of light, that concept can be correctly applied to understand why objects can approach, but not reach, the speed of light, but it falls apart as soon as you incorporate massless particles, like photons.
It’s far better to understand the laws of relativity as they actually are than to try and shoehorn them into a more intuitive box whose applications are fundamentally limited and restrictive. Just as is the case with quantum physics, until you’ve spent enough time in the world of relativity to gain an intuition for how things work, an overly simplistic analogy will only get you so far. When you reach its limits, you’ll wish you had learned it correctly and comprehensively the first time, all along.