How Many Fundamental Constants Does It Take To Explain The Universe?

And, even with all we know, what still remains unexplained?
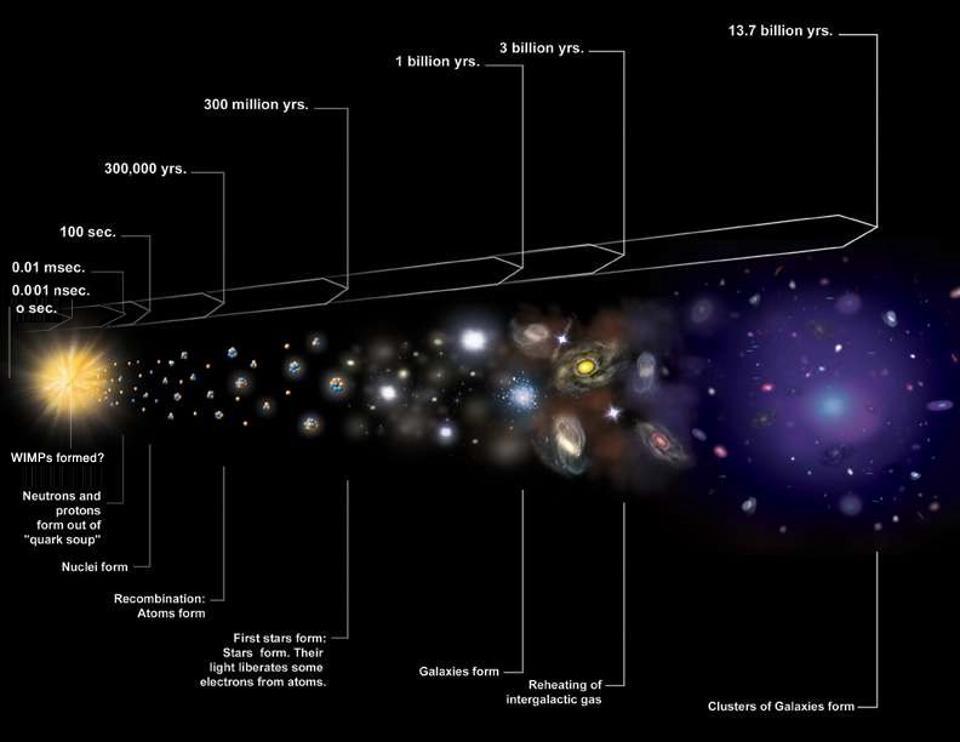
At a fundamental level, our Universe is made of particles, forces, interactions, and the fabric of space and time. Spacetime forms the ever-evolving stage on which the play of the cosmos unfolds, while the particles are the players. They can bind together, collide, annihilate, repel, attract, or otherwise interact according to the rules that govern the laws of nature. These pieces of information, along with the initial conditions of what was present in our Universe a long time ago, gives us almost everything we need to understand how the Universe came to be the way it is today.
The one missing ingredient? The fundamental constants that describe the strengths of all the interactions and the physical properties of all the particles. We need those pieces of information to understand the Universe quantitatively, and answer the question of “how much.” It takes 26 fundamental constants to give us our known Universe, and even with them, they still don’t give us everything.
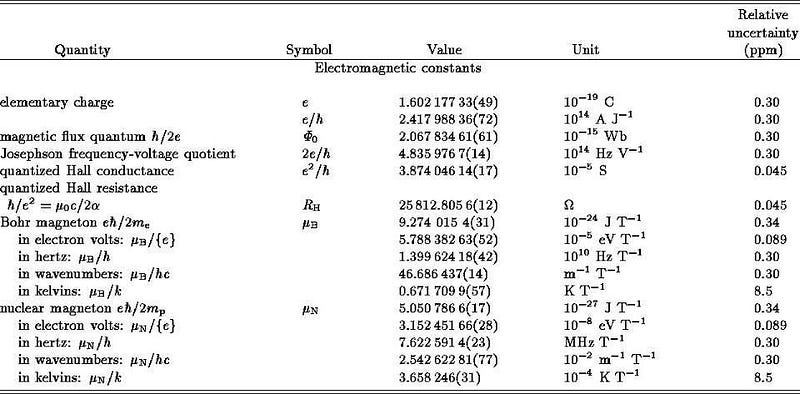
Think about any particle at all, and how it might interact with another. An electron, for instance, might interact with another electron. It has a fundamental charge associated with it, qe, and a fundamental mass, me. The electrons will gravitationally attract one another proportional to the strength of the gravitational force, G, and will repel one another electromagnetically, inversely proportional to the strength of the permittivity of free space, ε0. There are other constants that play a major role in how these particles behave as well, like the speed of light, c, and the fundamental constant associated with quantum transitions: Planck’s constant, ħ.
But physicists don’t like to use these constants when we describe the Universe, because these constants have arbitrary dimensions and units to them.
There’s no inherent importance to a unit like a meter, a kilogram or a second. We could work in any units we liked, and the laws of physics would behave exactly the same. In fact, we can frame everything we’d ever want to know about the Universe without defining a fundamental unit of “mass” or “time” or “distance” at all. We could describe the laws of nature, entirely, by using solely constants that are dimensionless.
Dimensionless is a simple concept: it means a constant that’s just a pure number, without meters, kilograms, seconds or any other “dimensions” in them. If we go that route to describe the Universe, and get the fundamental laws and initial condition correct, we should naturally get out all the measurable properties we can imagine. This includes things like particle masses, interaction strengths, cosmic speed limits, and even the fundamental properties of spacetime.

If we want to describe the Universe as simply and completely as possible, it takes 26 dimensionless constants to get us there. This is quite a small number, but not necessarily as small as we’d like. In an ideal world, at least from the point of view of most physicists, we’d like to think that these constants arise from somewhere physically meaningful, but no current theory predicts them.
With all that said, here’s what those 26 constants that give us the Universe as-we-know-it are.
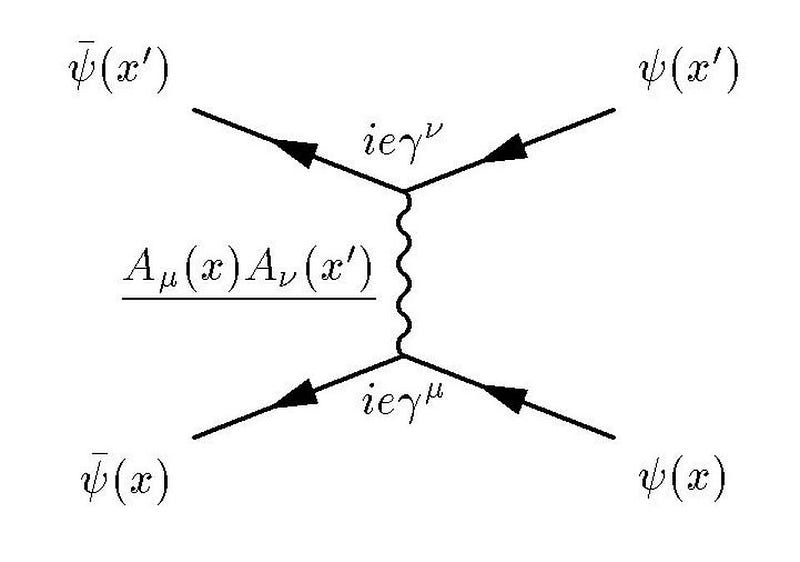
1.) The fine-structure constant, or the strength of the electromagnetic interaction. In terms of some of the physical constants we’re more familiar with, this is a ratio of the elementary charge (of, say, an electron) squared to Planck’s constant and the speed of light. But if you put these constants together, you get a dimensionless number! At the energies currently present in our Universe, this number comes out to ≈ 1/137.036, although the strength of this interaction increases as the energy of the interacting particles rise.
2.) The strong coupling constant, which defines the strength of the force that holds protons and neutrons together. Although the way the strong force works is very different from the electromagnetic force or gravity, the strength of this interaction can still be parametrized by a single coupling constant. This constant of our Universe, too, like the electromagnetic one, changes strength with energy.
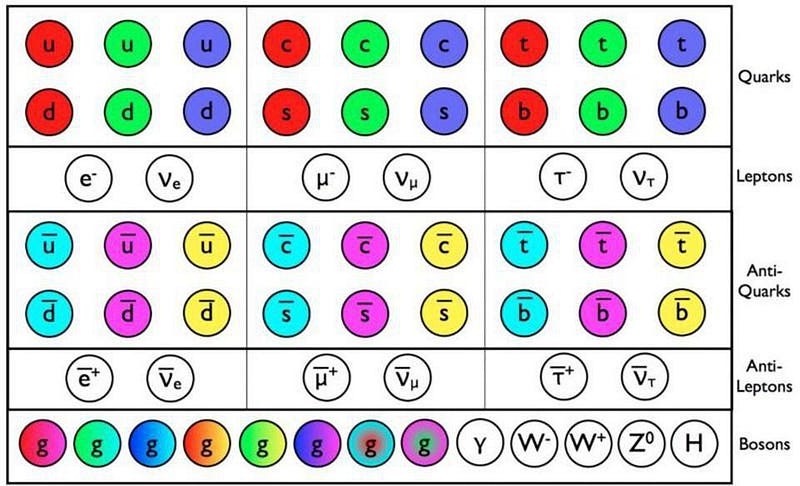
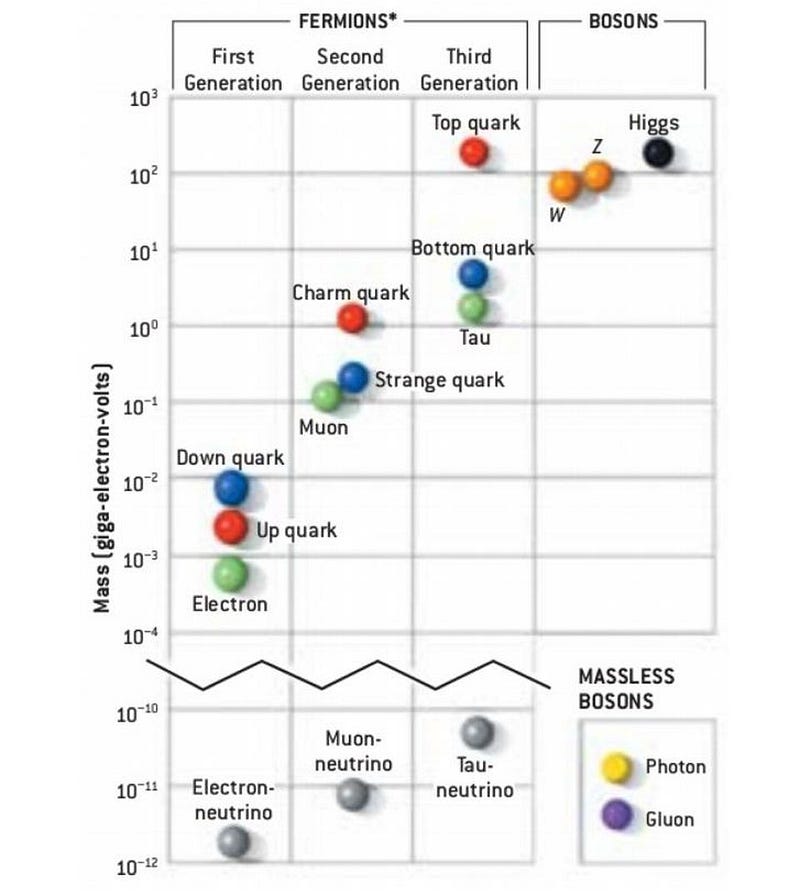
3–17.) The masses of the six quarks, six leptons, and three massive bosons. This one is a bit of a disappointment. We have fifteen particles in the Standard Model: the six quarks, six leptons, the W, Z, and the Higgs bosons, all of which have a substantial rest mass. While it’s true that their antiparticles all have identical rest masses, we were hoping that there would’ve been some relationship, pattern, or more fundamental theory that gave rise to these masses with fewer parameters.

There may yet be, as some weird almost-perfect relations can be derived: collide a positron at 45 GeV with an electron at 45 GeV, and you have the right amount of energy to make a Z boson; collide a positron at 45 GeV with an electron at rest, and you have the right amount of energy to make a muon/anti-muon pair. Unfortunately, this relation is approximate and not exact; the energy to create a Z-boson is closer to 46 GeV; the energy to make a muon/anti-muon pair is closer to 44 GeV. If there is a true underlying theory that describes our particle masses, we have yet to discover it.
As a result, it takes fifteen constants to describe the known masses. The lone good news is that we can save ourselves another constant. By scaling these mass parameters to be relative to the gravitational constant, G, we wind up with 15 dimensionless parameters without requiring a separate descriptor of the gravitational force’s strength.
18–21.) The quark mixing parameters. We have six different types of quarks, and because there are two subsets of three that all have the same quantum numbers as one another, they can mix together. If you’ve ever heard of the weak nuclear force, radioactive decay, or CP-violation, these four parameters — all of which must be (and have been) measured — are required to describe them.
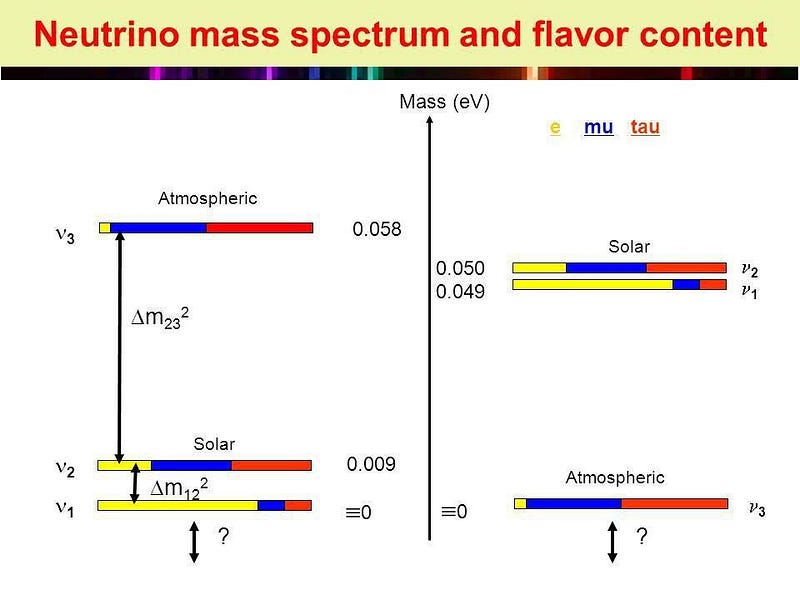
22–25.) The neutrino mixing parameters. Similar to the quark sector, there are four parameters that detail how neutrinos mix with one another, given that the three types of neutrino species all have the same quantum number. Although physicists initially hoped that neutrinos would be massless and not require additional constants, nature had other plans. The solar neutrino problem — where only a third of the neutrinos emitted by the Sun were arriving here on Earth — was one of the 20th century’s biggest conundrums.
It was only solved when we realized that neutrinos:
- had very small but non-zero masses,
- mixed together,
- and oscillated from one type into another.
The quark mixing is described by three angles and one CP-violating complex phase, and the neutrino mixing is described in the same way. While all four parameters have already been determined for the quarks, the CP-violating phase for the neutrinos remains unmeasured.
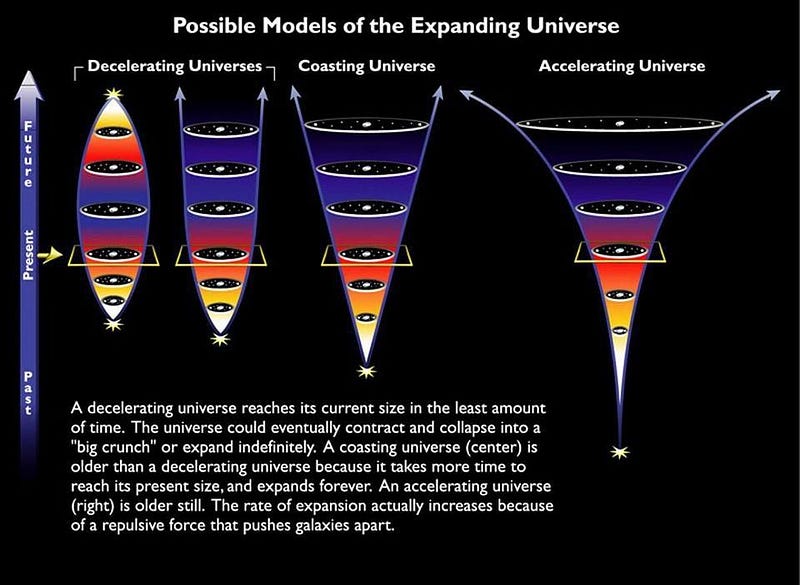
26.) The cosmological constant. You may have heard that the Universe’s expansion is accelerating due to dark energy, and this requires yet one more parameter — a cosmological constant — to describe the amount of that acceleration. Dark energy could yet turn out to be more complex than being a constant, in which case it may need more parameters as well, and hence the number may be greater than 26.
If you give a physicist the laws of physics, the initial conditions of the Universe, and these 26 constants, they can successfully simulate any aspect of the entire Universe. And quite remarkably, what you’ll get out looks pretty much indistinguishable from the Universe we have today, from the smallest, subatomic scales all the way up to the largest, cosmic ones.
Well, almost.
Even with this, there are still four puzzles that may yet require additional constants to solve. These are:
- The problem of the matter-antimatter asymmetry. The entirety of our observable Universe is made up dominantly of matter and not antimatter, yet we do not fully understand why this is so, or why our Universe has the amount of matter it does. This problem, known as baryogenesis, is one of the great unsolved problems in theoretical physics, and may require one (or more) new fundamental constants to describe its solution.
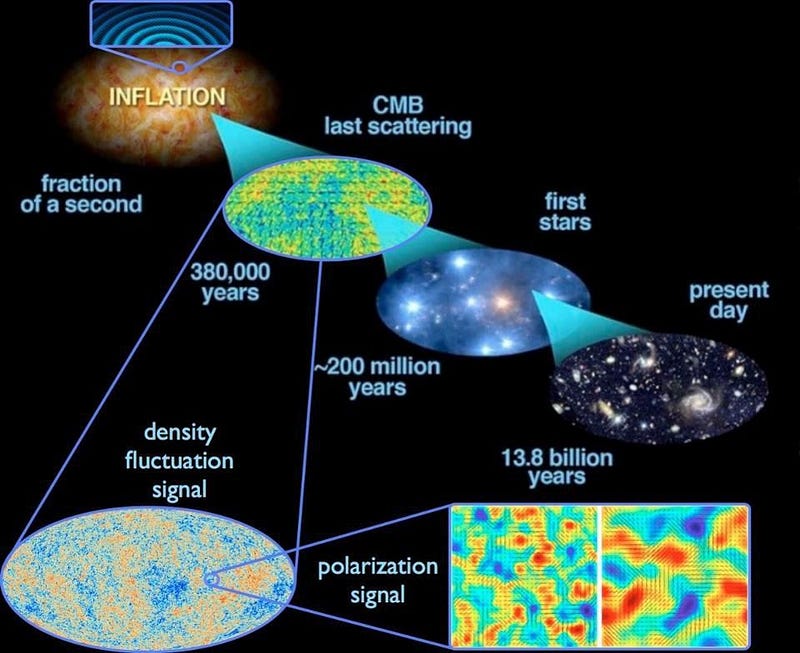
- The problem of cosmic inflation. This is the phase of the Universe that preceded and set up the Big Bang has made many new predictions that have been verified observationally, but isn’t included in this description. Very likely, when we more fully understand what this is, additional parameters will have to be added to this set of constants.
- The problem of dark matter. Given that it almost definitely consists of at least one (and maybe more) new type of massive particle, it stands to reason that more new parameters will need to be added. The complexity of dark matter will determine the actual number of constants needed, but it’s safe to say that at least one new one, and possibly many more, will likely be required.
- The problem of strong CP-violation. We see CP-violation in the weak nuclear interactions and expect it in the neutrino sector, but we have yet to find it in the strong interactions, even though it is not forbidden. If it exists, there should be more parameters; if it doesn’t, there is likely an additional parameter related to the process that restricts it.
Our Universe is an intricate, amazing place, and yet our greatest hopes of a unified theory — a theory of everything — seek to decrease the number of fundamental constants we need. In reality, though, the more we learn about the Universe, the more parameters we’re learning it takes to fully describe it. It’s important to recognize where we are and what it takes, today, to describe the entirety of what’s known.
But we still don’t know everything, and so it’s also important to keep searching for a more complete paradigm. If we’re successful, it will give us absolutely everything the Universe has in it, including solutions to our current mysteries. The hope of many, but not a requirement, is that the Universe will wind up being simpler than we currently know. Right now, unfortunately, anything simpler than what’s been put forth here is too simple to work. Our Universe may not be elegant, after all.
Ethan Siegel is the author of Beyond the Galaxy and Treknology. You can pre-order his third book, currently in development: the Encyclopaedia Cosmologica.