Without Einstein, we might have missed General Relativity

Back in the late 1800s, what we thought of as “fundamental science” was rapidly advancing, leading to two different conflicting perspectives. Among most of the old guard, Maxwell’s theory of electromagnetism represented a spectacular achievement: making sense of electricity and magnetism as a single, unified phenomenon. Along with Newtonian gravity and the mechanical laws of motion, it seemed that everything in the Universe could soon be explained. But many others, including many young and emerging scientists, saw precisely the opposite: a Universe on the verge of a crisis.

At speeds approaching the speed of light, time dilation and length contraction violated Newton’s laws of motion. When we tracked the orbit of Mercury over centuries, we found that its precession deviated from the Newtonian prediction by a small but significant amount. And phenomena like radioactivity simply couldn’t be explained within the existing framework.

The coming decades would see many revolutionary developments take place: special relativity, quantum mechanics, mass-energy equivalence, and nuclear physics among them. But perhaps the most imaginative leap forward was Einstein’s General Relativity, which only came about because of one key realization. If things had played out just slightly differently, we might still be chasing after that game-changing theoretical insight today.

This 1934 photograph shows Einstein in front of a blackboard, deriving special relativity for a group of students and onlookers. Although special relativity is now taken for granted, it was revolutionary when Einstein first put it forth, and doesn’t even describe his most famous equation, which is E = mc².

1905 is rightfully known in the history of science as Einstein’s “miracle year.” In a series of papers all published in that year, Einstein, in one fell swoop, changed how we saw the Universe. At speeds close to the speed of light, we had already known that lengths contracted and time dilated thanks to the work of George FitzGerald and Hendrik Lorentz, but it was Einstein who realized that the speed of light was the one unchanging constant for everyone, leading him to formulate the special theory of relativity.

Contemporaneously, Einstein published his important works on:

• E = mc², establishing the equivalence between mass and energy,
• the photoelectric effect, establishing the quantization of light into discrete energy packets known as photons,
• and Brownian motion, establishing the rules that described microscopic particles’ motions in real-time.

This led the entire field of physics to many important subsequent developments, by both Einstein and also by others. But the biggest open question still remained: what was going on with the orbit of Mercury, and why? For hundreds of years, since the time of Tycho Brahe, we had tracked the perihelion of Mercury as it approached the Sun at its closest, and found something shocking: unlike the predictions of Newtonian gravity, Mercury did not return to the same place with each completed orbit!

This illustration shows the precession of a planet’s orbit around the Sun. A very small amount of precession is due to general relativity in our Solar System; Mercury precesses by 43 arc-seconds per century, the greatest value of all our planets. Although the total rate of precession is 5600 arc-seconds per century, 5025 of them are due to the precession of the equinoxes and 532 are due to the effects of the other planets in our Solar System. Those final 43 arc-seconds per century cannot be explained without general relativity.

This was a bit of a puzzle. Under the laws of Newtonian gravity, any negligibly small mass in a stable gravitational orbit around a large, unmoving one would have to make a closed ellipse: returning to its exact same starting point upon completing each revolution. However, there were two known factors that should complicate this about the planet Mercury’s orbit as observed from Earth.

1. Planet Earth has equinoxes, and those equinoxes precess as our rotation axis migrates over time. With each passing century, this accounts for 5025 arc-seconds of precession, where 3600 arc-seconds makes up 1°.
2. There are other masses in the Solar System that also exert gravitational forces on all of the other masses, leading to an additional precession effect. From the seven other major planets, Venus through Neptune, Mercury gains an additional 532 arc-seconds of precession per century.

All told, that’s a predicted precession of 5557 arc-seconds per century. And yet, even in the early 1900s, we had conclusively determined that the observed precession was more like 5600 arc-seconds per century, with an uncertainty of less than 0.1% in that figure. Newtonian gravity, somehow, was still failing us.

The hypothetical location of the planet Vulcan, presumed to be responsible for the observed precession of Mercury in the 1800s. Exhaustive searches were performed for a planet that could have accounted for the anomalous motions of Mercury in the context of Newtonian gravity, but no such planet exists, falsifying the prediction of an interior planet in our Solar System, general relativity, a different theory of gravity, instead explains this otherwise anomalous precession.

A lot of clever ideas came about in various attempts to solve this problem and account for the additional observed precession. Perhaps, thought many, there was an additional planet, hitherto undiscovered, interior to Mercury, and that its gravitational influence was causing the precession we were seeing. This clever idea came about in the mid-1800s, and was so popular that the hypothetical planet even got a name: Vulcan. Yet despite exhaustive searches, no object was ever found. Vulcan, quite simply, does not exist.

Other ideas included modifying Newton’s gravity. Simon Newcomb and Asaph Hall took Newton’s law of gravitation and decided to modify the exponent attached to the inverse-square force law — the “2” in the 1/r part of Newtonian gravity — to account for Mercury’s precession. Instead of being exactly 2, they noted that if the exponent in the force law were changed to “2 + ε,” where ε (the Greek letter epsilon) was some tiny number that could be tuned to match the observations, Mercury’s perihelion precession could be explained without messing up the orbits of any of the other planets. It was a clever, but ultimately incorrect and insufficient, approach.

A mural of the Einstein field equations, with an illustration of light bending around the eclipsed Sun: the key observations that first validated general relativity four years after it was first theoretically put forth: back in 1919. The Einstein tensor is shown decomposed, at left, into the Ricci tensor and Ricci scalar, with the cosmological constant term added in after that. If that constant weren’t included, an expanding (or collapsing) Universe would have been an inevitable consequence.

With special relativity now established, two important advances occurred, arguably leading Einstein to the most important realization of his life.

1. Einstein’s former professor, Hermann Minkowski, came up with a mathematical formalism where space and time were no longer treated separately but woven into a single fabric: spacetime. As one moved through space more rapidly, they moved through time more slowly, and vice versa. The factor that related space to time was none other than the speed of light, and this formulation saw the equations for special relativity — including length contraction and time dilation — emerge intuitively.
2. Henri Poincaré, a contemporary of Einstein, noted that if you took into account the speed at which Mercury (the fastest of all the planets) orbited the Sun and applied special relativity to it, you’d obtain a step in the right direction: an additional precession of 7 arc-seconds per century.

Although we’ll never know for certain just how responsible they were, it’s probable that both of these subsequent developments influenced Einstein tremendously, leading him to an insight that he would later call “his happiest thought” of his life: the equivalence principle.

The identical behavior of a ball falling to the floor in an accelerated rocket (left) and on Earth (right) is a demonstration of Einstein’s equivalence principle. If inertial mass and gravitational mass are identical, there will be no difference between these two scenarios. This has been verified to better than ~1 part in one trillion for matter through torsion balance experiments, and was the thought (Einstein called it “his happiest thought”) that led Einstein to develop his general theory of relativity. Recently, the ALPHA-g experiment confirmed that this is true for antimatter as well.

Einstein imagined being in some sort of a room, with that room accelerating through space. Then he asked himself what sort of measurement, if any, could he make from within that room that would distinguish that accelerating room-in-motion from an identical room that was stationary, but in a gravitational field?

His spectacular realization — that there would be none — led him to the conclusion that what we experienced as gravity wasn’t a “force” at all in the old, Newtonian, action-at-a-distance sort of sense. Instead, just as objects in motion relative to one another experienced their passage through space and time differently, gravitation must represent some sort of alteration for how an observer experienced the spacetime through which they passed. (Technically, of course, balls dropped on either side of the room would fall “down” in an accelerating room but “toward the center of mass” in a gravitational field; if one could detect that difference, you could distinguish them after all!)

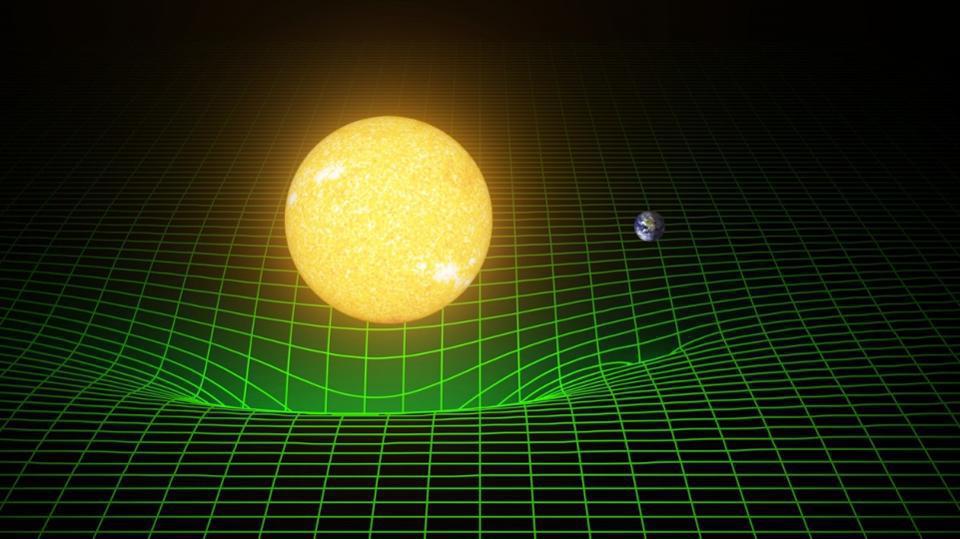
In our reality, the rest was history. Einstein went off, enlisted the help of others, and mathematically began thinking of how the presence of matter-and-energy would curve and distort the very fabric of spacetime. In 1915, this culminated in the release of General Relativity in its final form. Mass (and energy) told spacetime how to curve, and that curved spacetime told all matter and energy how to move through it.

The gravitational behavior of the Earth around the Sun is not due to an invisible gravitational pull, but is better described by the Earth falling freely through curved space dominated by the Sun. The shortest distance between two points isn’t a straight line, but rather a geodesic: a curved line that’s defined by the gravitational deformation of spacetime. The notion of “distance” and “time” is unique for every observer, but under Einstein’s description, all frames of reference are equally valid, and the “spacetime interval” remains an invariant quantity.

But there was another direction that Einstein — or perhaps someone else — could have gone in: to make an even stronger analogy with electromagnetism than had previously been tried.

Newtonian gravity was a lot like Coulomb’s law for the electric force in electromagnetism, where a stationary charge (or mass, in the case of gravity) attracts or repels (or only attracts, in the case of gravity) any other charge in proportion to their mutual charges (or masses, for gravity) and inversely proportional to the distance squared between those two objects.

But what if there was also, in addition to that, an analogy to the magnetic force in electromagnetism? There could be a gravitational analogy to the magnetic part of the Lorentz force: where the product of a charge-in-motion moving through the magnetic field produces a force that’s different from, but in addition to, the electric force. For masses instead of charges, that would translate to a mass-in-motion moving through a gravitational field instead of a charge-in-motion moving through a magnetic field. Remarkably, this idea was also suggested by Henri Poincaré: in the same work where he calculated special relativity’s contribution to the precession of Mercury.

Polarized view of the black hole in M87. The lines mark the orientation of polarization, which is related to the magnetic field around the shadow of the black hole. Note how much “swirlier” this image appears than the original, which was more blob-like. It’s fully expected that all supermassive black holes will exhibit polarization signatures imprinted upon their radiation, a calculation that requires the interplay of General Relativity with electromagnetism to predict.

In fact, if you perform exactly this calculation, you get a “correction” term to Newtonian gravity: one that depends on the ratio of the moving object’s velocity, squared, to the speed of light, squared. You can simply adjust the constant that you calculate out in front of this term to get it to match observations.

Similarly, you could also have modified Newtonian gravity to, instead of having a gravitational potential that scales as ~1/r, to add in an additional term that scales as ~1/r³. Again, you’d have to tune your results to get the right constant out in front, but it could be done.

Under this ad hoc approach, however, we could have solved many of the greatest problems of the day. We could have explained Mercury’s orbit. Gravitational time dilation would have been predicted as well, while additional “corrections” would have been needed for things like the Lens-Thirring effect, for the properties of gravitational waves, and for gravitational lensing and the deflection of starlight. We might have been able to explain and describe them all, but it would be much like a series of epicycles, rather than a fully predictive, successful framework like the one provided by General Relativity.

An animated look at how spacetime responds as a mass moves through it helps showcase exactly how, qualitatively, it isn’t merely a sheet of fabric. Instead, all of 3D space itself gets curved by the presence and properties of the matter and energy within the Universe. Space doesn’t “change shape” instantaneously, everywhere, but is rather limited by the speed at which gravity can propagate through it: at the speed of light. The theory of general relativity is relativistically invariant, as are quantum field theories, which means that even though different observers don’t agree on what they measure, all of their measurements are consistent when transformed correctly.

In science, finding one fix that works for one problem (or a small set of similar problems) among many isn’t the way our understanding of the Universe advances. Sure, it may make us feel better when we have a successful description of things, but getting the right answer for the wrong reason can often lead us even farther astray than not being able to obtain the right answer at all.

The hallmark of a good scientific theory is that it can explain:

• a wide variety of existing observations,
• across a broad range of timescales, distance scales, energy scales, and other physical conditions,
• can make new predictions that differ from the previously prevailing theory,
• and that those predictions can be put to the test, either validating it or refuting it,

while introducing the fewest number of new free parameters possible. Today, a Universe governed by General Relativity, that began with an inflationary state that gave rise to the hot Big Bang, and that contains some form of dark matter and dark energy in addition to the “normal stuff,” is the most remarkably successful picture we’ve ever concocted. But as awesome as our successes are, we’re still searching for a better, more successful description of reality. Whether there is one or not, the only way we’ll find out is to keep on trying, and letting nature itself be the ultimate arbiter of the only important question we can ask: what is true?