Did We Just Find The Largest Rotating ‘Thing’ In The Universe?

Filaments, hundreds of millions of light-years long, were just caught spinning.
In our own cosmic backyard, everything we see spins, rotates, and revolves in some fashion or other. Our planet (and everything on it) spins about its axis, just like every planet and moon in the Solar System. The moons (including our own) revolve around their parent planet, while the planet-moon systems all revolve around the Sun. The Sun, in turn, like all of the hundreds of billions of stars in the galaxy, orbit around the galactic center, while the entire galaxy itself spins about the central bulge.
On the largest of cosmic scales, however, there’s no observed global rotation. The Universe, for whatever reason, doesn’t appear to have an overall spin or rotation to it, and doesn’t appear to be revolving around anything else. Similarly, the largest observed cosmic structures don’t appear to be spinning, rotating, or revolving around any other structures. But recently, a new study appears to be challenging that, claiming that enormous cosmic filaments — the strands of the cosmic web — appear to be rotating about the filamentary axis itself. This is weird, for sure, but can we explain it? Let’s find out.

In order to make a prediction, we first have to set up the scenario that we expect, then put in the laws of physics, and evolve the system forward in time to see what we anticipate. We can go all the way back, theoretically, to the earliest stages of the Universe. At the start of the hot Big Bang, immediately following the end of cosmic inflation, the Universe is:
- filled with matter, antimatter, dark matter, and radiation,
- uniform and the same in all directions,
- with the exception of slight density imperfections on the scale of 1-part-in-30,000,
- and with additional tiny imperfections in the directionality of these fluctuations, the linear and rotational motions of these overdense and underdense regions, and similar imperfections in gravitational wave background that the Universe is born with.
As the Universe expands, cools, and gravitates, a number of important steps occur, particularly on large cosmic scales.
In particular, some things grow with time, other things decay with time, and still other things remain the same with time.
The density imperfections, for example, grow in a particular fashion: proportional to the ratio of the matter density to the radiation density. As the Universe expands and cools, both matter and radiation — made up of individual quanta — get less dense; the number of particles remains the same while the volume increases, causing the density of both to drop. They don’t drop equally, however; the amount of mass in every matter particle remains the same, but the amount of energy in every quantum of radiation drops. As the Universe expands, the wavelength of the light traveling through space stretches, bringing it to lower and lower energies.
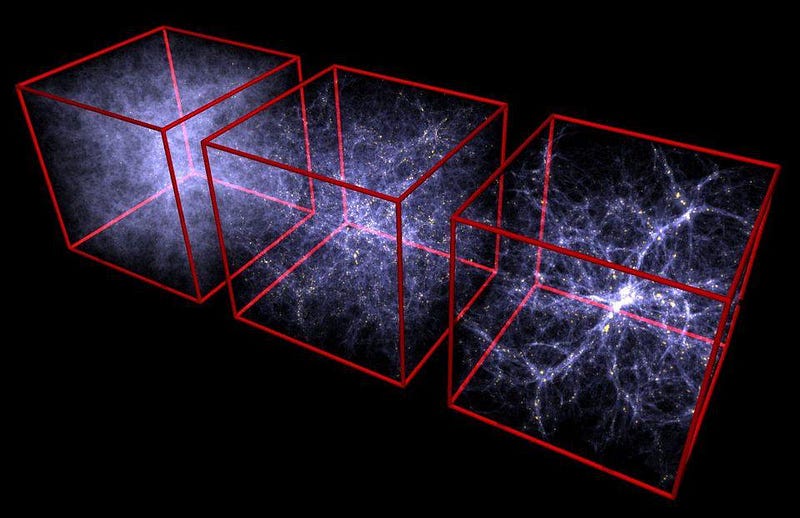
As the radiation gets less energetic, the matter density rises relative to the radiation density, causing these density imperfections to grow. Over time, the initially overdense regions preferentially attract the surrounding matter, drawing it in, while the initially underdense regions preferentially give up their matter to the denser regions nearby. Over long enough timescales, this leads to the formation of molecular gas clouds, stars, galaxies, and even the entire cosmic web.
Similarly, you can track the evolution of any initial rotational modes in a Universe that’s initially isotropic and homogeneous. Unlike the density imperfections, which grow, any initial spin or rotation will decay away as the Universe expands. Specifically, it decays as the scale of the Universe grows: the more the Universe expands, the less important angular momentum becomes. It should make sense, therefore, to anticipate that there won’t be any angular momentum — and hence, any spinning or rotation — on the largest cosmic scales.
At least, that’s true, but only up until a certain point. As long as your Universe, and the structures in it, continue to expand, these rotational or spinning modes will decay away. But there’s a rule that’s even more fundamental: the law of conservation of angular momentum. Just like a spinning figure skater can increase their rate of rotation by bringing their arms and legs in (or can decrease it by moving their arms and legs out), the rotation of large-scale structures will diminish so long as the structures expand, but once they get pulled in under their own gravity, that rotation speeds up again.

Angular momentum, you see, is a combination of two different factors multiplied together.
- Moment of inertia, which you can think about as how your mass is distributed: close to the rotation axis is a small moment of inertia; far away from the rotation axis is a large moment of inertia.
- Angular velocity, which you can think of as how quickly you make a complete revolution; something like revolutions-per-minute is a measure of angular velocity.
Even in a Universe where your density imperfections are born only with a very slight amount of angular momentum, gravitational growth won’t be able to get rid of it, while gravitational collapse, which causes your mass distribution to get concentrated towards the center, ensures that your moment of inertia will eventually decrease dramatically. If your angular momentum stays the same while your moment of inertia goes down, your angular velocity must rise in response. As a result, the greater the amount of gravitational collapse a structure has undergone, the greater the amount we expect to see it spinning, rotating, or otherwise manifesting its angular momentum.

But even that is only half of the story. Sure, we fully expect that the Universe is born with some angular momentum, and when these density imperfections grow, attract matter, and finally collapse under their own gravity, we expect to see them rotating — perhaps even quite substantially — in the end. However, even if the Universe were born with no angular momentum anywhere at all, it’s an inevitability that the structures that form on all cosmic scales (except, perhaps, the extreme largest ones of all) will start spinning, rotating, and even revolving around one another.
The reason for this is a physical phenomenon we’re all familiar with, but in a different context: tides. The reason planet Earth experiences tides is because the objects near it, like the Sun and the Moon, gravitationally attract the Earth. Specifically, however, they attract every point on the Earth, and they do so unequally. The points on the Earth that are closer to the Moon, for instance, get attracted a little bit more than the points that are farther away. Similarly, the points that are “north” or “south” of the imaginary line that connects Earth’s center to the Moon’s center will be attracted “downward” or “upward” correspondingly.
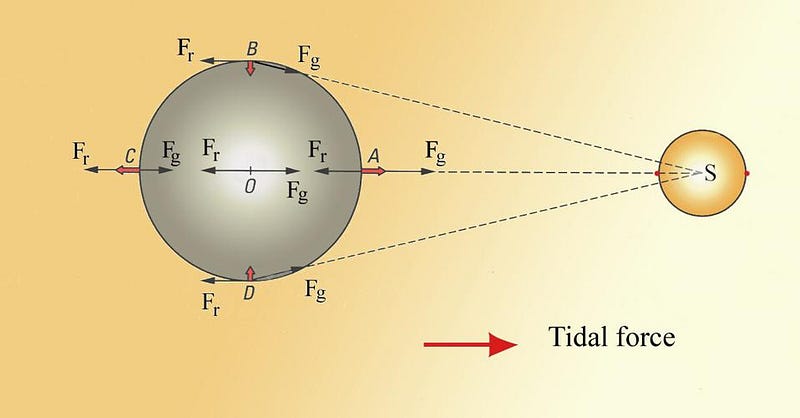
Despite how easy this is to visualize for a round body like the Earth, the same process takes place between every two masses in the Universe that occupy any volume more substantial than a single point. These tidal forces, as objects move through space relative to one another, exerts what’s known as a torque: a force that causes objects to experience a greater acceleration on one part of it than other parts of it. In all but the most perfectly aligned cases — where all the torques cancel out, a tremendous and coincidental rarity — these tidal torques will cause an angular acceleration, leading to an increase in angular momentum.
“Hang on,” I can hear you objecting. “I thought you said that angular momentum was always conserved? So how can you create an angular acceleration, which increases your angular momentum, if angular momentum is something that can never be created or destroyed?”
It’s a good objection. What you have to remember, however, is that torques are just like forces in the sense that they obey their own versions of Newton’s laws. In particular, just like forces have directions, so do torques: they can cause something to rotate clockwise or counterclockwise about each of the three-dimensional axes that exist in our Universe. And just like every action has an equal an opposite reaction, whenever one object pulls on another to create a torque, that equal and opposite force will create a torque on that first object as well.

It’s not something you think of very often, but this plays out all the time in our reality. When you accelerate your automobile from a standstill as soon as the light turns green, your tires start to spin and push against the road. The road, therefore, exerts a force on the bottom of your tires, which causes your spinning tires to grip the road, accelerate, and push the car forward. Because the force isn’t directly on the center of the wheels — where the axels are — but rather off-center, your tires spin, gripping the road, and creating a torque.
But there’s an equal-and-opposite reaction here, too. The road and the tires have to push on one another with equal and opposite forces. If the force of the road on the tires causes your automobile to accelerate and then move, say, clockwise with respect to the center of planet Earth, then the force of the tires on the road will cause planet Earth to accelerate and rotate, ever so slightly, a little bit extra in the counterclockwise direction with respect to how it was moving before. Even though:
- the car now has more angular momentum than it did before,
- and the Earth now has more angular momentum than it did before,
the sum of the car+Earth system has the same amount of angular momentum as it did initially. Angular momentum, like force, is a vector: with magnitude and direction.

So what happens, then, when the large-scale structure in the Universe forms?
As long as you’re not too large for gravitational collapse to occur — where matter in the Universe can contract all the way down in one or more dimension to a scale where things will go “splat” due to collisions — these tidal torques will cause clumps of matter to pull on one another, inducing a rotation. This means that planets, stars, solar systems, galaxies, and even, in theory, entire cosmic filaments from the cosmic web should, at least sometimes, experience rotational motions. On larger scales, however, there should be no overall rotation, as there are no larger bound structures in the Universe.
This is precisely what the latest study sought to measure, and precisely what they found. For individual filaments, they couldn’t see anything, but when they took thousands of filaments together, the rotational effects clearly showed up.
“By stacking thousands of filaments together and examining the velocity of galaxies perpendicular to the filament’s axis (via their redshift and blueshift), we find that these objects too display vortical motion consistent with rotation, making them the largest objects known to have angular momentum. The strength of the rotation signal is directly dependent on the viewing angle and the dynamical state of the filament. Filament rotation is more clearly detected when viewed edge-on.”

We’ve seen “filament rotation” before: in the filaments that are created in star-forming regions within individual galaxies. But in a surprise to some, even the largest-scale filaments in the Universe, the ones that trace the cosmic web, appear to be rotating as well, at least on average. Their speeds are comparable to the speeds at which galaxies move and stars orbit within the Milky Way: up to ~hundreds of kilometers per second. Even though there’s a lot we still have left to unpack about this phenomenon, these large-scale cosmic filaments, which typically extend for hundreds of millions of light-years, are now the largest known rotating structures in the Universe.
Why are they rotating, however? Is it something that can truly be explained by tidal torques and nothing else? The early evidence points to “yes,” as the presence of large masses near the filaments — what cosmologists identify as “haloes” — seems to intensify the rotation. As the authors note, “the more massive the haloes that sit at either end of the filaments, the more rotation is detected,” consistent with gravitational torques inducing these motions. Nevertheless, more study is needed, as temperature and other physics may also play a role.
The big breakthrough is that we’ve finally detected rotation on these unprecedentedly large scales. If all goes well, we’ll not only figure out why, but we’ll be able to predict how quickly each filament that we see ought to be spinning, and for what reason. Until we can predict how every structure in the Universe forms, behaves, and evolves, theoretical astrophysicists will never run out of work to do.
Starts With A Bang is written by Ethan Siegel, Ph.D., author of Beyond The Galaxy, and Treknology: The Science of Star Trek from Tricorders to Warp Drive.





