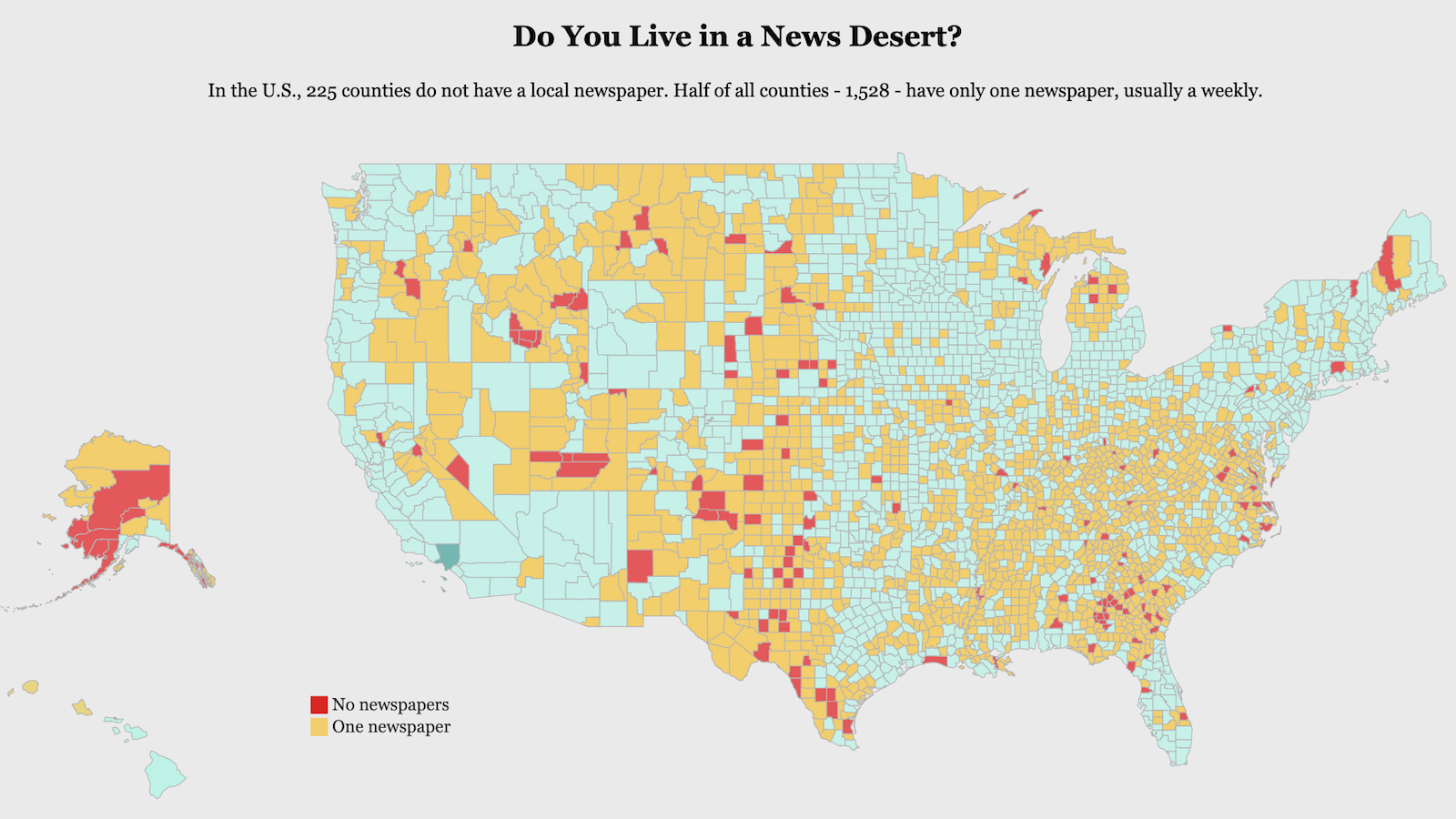
Ask Ethan: Why is there a limit to what physics can predict?

There’s a smallest scale and a shortest time at which physics makes any sense. What sets that limit?
“There is a limit on how much information you can keep bottled up.”
–Dick Gregory
If you divide the matter in the Universe into smaller and smaller constituents, you’ll eventually reach a limit when you hit a fundamental, indivisible particle. All macroscopic objects can be divided into molecules, then atoms, then electrons (which are fundamental) and nuclei, then protons and neutron, and finally, inside them, there are quarks and gluons. Electrons, quarks and gluons are examples of fundamental particles that cannot be divided any smaller. But how is it possible that space and time itself have those very same limits? Derek Kueter wants to know:
Why are there these units (Planck units) which you can’t further divide?
To understand where a Planck unit comes from, you need to think about the two laws that govern reality: General Relativity and Quantum Physics.

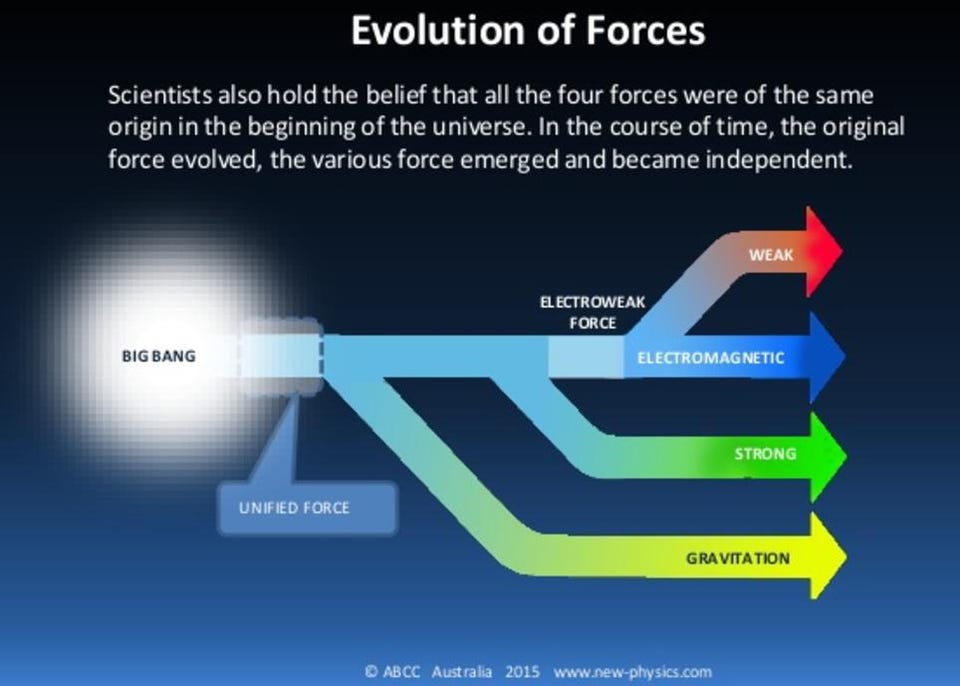
General Relativity relates the matter and energy present in the Universe to the curvature and deformation of the fabric of spacetime. Quantum physics describes how different particles and fields interact with one another within the fabric of spacetime, including on very small scales. There are two fundamental, physical constants that play a role in General Relativity: G, the gravitational constant of the Universe, and c, the speed of light. G appears because it sets the amount that spacetime deforms due to matter and energy; c appears because the gravitational interaction propagates through spacetime at the speed of light.
In quantum mechanics, there are also two fundamental constants that appear: c and h, where the latter is Planck’s constant. c is the speed limit of all particles, the speed at which all massless particles must travel, and the fastest speed at which any interaction can propagate. Planck’s constant, h, was incredibly important for describing how quantum energy levels, interactions between particles, and the number of possible outcomes are quantized, or countable. An electron orbiting a proton can have any number of energy levels, but they occur in discrete steps, where the size of those steps are determined by h.

Put these three constants together: G, c, and h, and you can use various combinations of them to construct a length scale, a mass, and a time period. These are known, respectively, as the Planck length, the Planck mass, and the Planck time. (You can construct other quantities, too like a Planck energy, Planck temperature, and so on.) These are, quite generically, the length, mass, and time scales at which — in the absence of any other information — you’d expect quantum effects to become important. There are good reasons to believe this is true, and it’s pretty easy to see why.

Imagine you had a particle of a certain mass. You can ask yourself, “if my particle was this mass, how small of a volume would it need to be compressed into to become a black hole?” You can also ask, “if I had a black hole of this size, how long would it take a particle moving at the speed of light to traverse that same distance?” The Planck mass, Planck length and Planck time correspond to exactly those values: a black hole of the Planck mass has a physical size of the Planck length and would have a light-travel-time across that distance of the Planck time.

But the Planck mass is far, far more massive than any particle we’ve ever created; it’s some 10¹⁹ times heavier than the proton! The Planck length, similarly, is perhaps 10¹⁴ times smaller than any distance scale we’ve ever probed, while the Planck time is 10²⁵ times smaller than any direct measurement. These scales haven’t been directly accessible to us, but they are important for another reason: the Planck energy (which you can get by putting the Planck mass into E = mc²) is the scale at which quantum gravitational effects ought to become important.

That means at energies that high — or equivalently, time scales shorter than the Planck time or length scales smaller than the Planck length — our current laws of physics should break down. Quantum gravitational effects become important, meaning the predictions of General Relativity become unreliable. The curvature of space becomes very large, meaning the “background” we use to calculate quantum quantities is also unreliable. The energy/time uncertainty relation means that the uncertainties become larger than the things we know how to calculate. In short, physics as-we-know-it doesn’t work anymore.

This isn’t much of a problem for our Universe. These energy scales are 10¹⁵ times higher than the Large Hadron Collider can reach, approximately 100,000,000 times greater than the most energetic particles the Universe itself creates (the highest energy cosmic rays), and even a factor of about 10,000 higher than the Universe achieved immediately following the Big Bang. But if we wanted to probe these limits, there is one place where they might be important: at the singularities located at the centers of black holes.
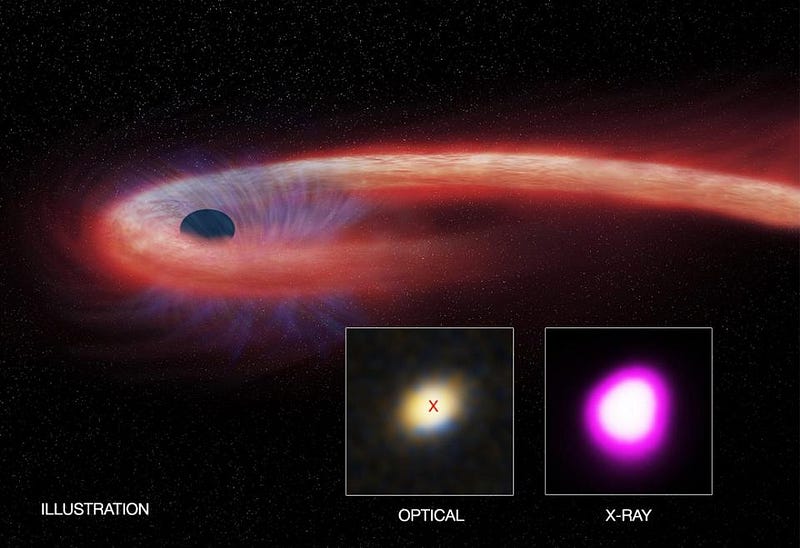
In these locations, masses far exceeding the Planck mass are compressed into a size that’s theoretically smaller than the Planck length. If there’s anyplace in the Universe where we cross these lines and enter into the Planck regime, this is it. We cannot access them today, because they’re shielded by a black hole’s event horizon, and are therefore inaccessible. But if we’re patient enough — and this requires a lot of patience — the Universe will give us our opportunity.

Black holes, you see, decay very slowly over time. The combination of quantum field theory in the curved spacetime of General Relativity means that a small amount of radiation is emitted in the space outside the event horizon, and the energy for that radiation comes out of the mass of the black hole. Over time, the black hole’s mass shrinks, the event horizon shrinks, and after about 10⁶⁷ years, a solar mass black hole will evaporate completely. If we could access all of the radiation leaving a black hole, including at those very final moments, we would undoubtedly be able to piece together whether there were any quantum effects that our current theories didn’t predict.

It isn’t necessarily the case that space is unable to be divided into smaller units than the Planck length, nor that time cannot be divided into units smaller than the Planck time. We simply know that our description of the Universe, including our laws of physics, cannot be all there is on those scales. Is space truly quantized? Is time fundamentally continuous, and flowing? And what do we make of the fact that all the known fundamental particles in the Universe have much, much smaller masses than the Planck mass? These are unsolved questions in physics. The Planck scale isn’t so much a fundamental limit to the Universe as it is a present limit in our understanding of the Universe. This is why we investigate! Perhaps, as our knowledge increases, the answers to the question of whether there’s a fundamental limit to space and time will someday emerge.
Send in your Ask Ethan questions to startswithabang at gmail dot com!
Ethan Siegel is the author of Beyond the Galaxy and Treknology. You can pre-order his third book, currently in development: the Encyclopaedia Cosmologica.