Ask Ethan: Why Don’t Gravitational Waves Get Weaker Like The Gravitational Force Does?

Gravity gets weaker as the distance squared. But gravitational waves only get weaker as the distance. Why?

One of the things we often just accept about the world is that physical effects get weaker the farther away we get from them. Light sources appear dimmer, the gravitational force gets weaker, magnets deflect by smaller amounts, etc. The most common way this arises is through an inverse-square law, meaning that if you double the distance between you and the source that creates the effect you’re measuring, the effect will be one quarter of what it was previously. But this isn’t true for gravitational waves, and that puzzles reader Jack Dectis, who asks:

You have stated:
1) The strength of gravity varies with the square of the distance.
2) The strength of gravity waves, as detected by LIGO, varies directly with the distance.
So the question is, how can those two be the same thing?

This is a real surprise to almost everyone when they hear about it, even professional physicists. But it’s true! Here’s the science of why.

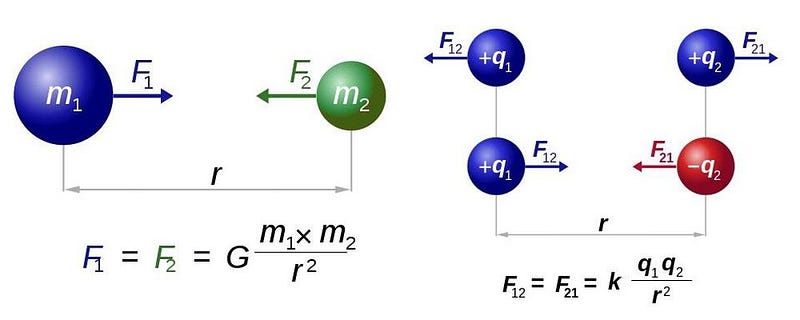
When you get near any other mass in the Universe, we typically view it as exerting a gravitational force on you. Sure, you also exert an equal and opposite gravitational force on it, but what you might be most interested in is the strength of that interaction. According to Newton, it’s a force that goes as 1/r²: a force that gets weaker the farther away you get from it.

Get twice as far, and it’s only a quarter as strong; get 10 times as far away, and it’s only 1% as strong. We call this an inverse square law, where its strength decreases with the square of the distance. At large distances, even when we go from Newton’s theory of gravity to Einstein’s theory of General Relativity, this remains true.

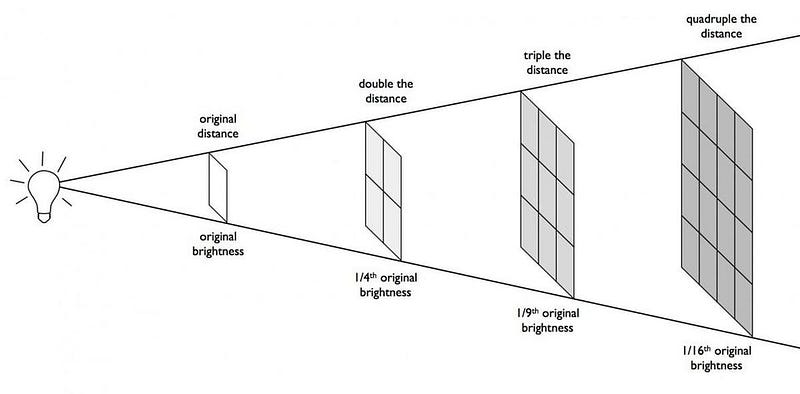
This is how most long-range forces work. The gravitational force works this way. The electric force works this way. And another important phenomenon you might be familiar with works this way, too: light. Any light source in the Universe will have a specific luminosity that’s inherent to it: an intrinsic brightness. But what you see as brightness — what we call apparent brightness — will depend on your distance from the light source.

How does brightness work as a function of distance? Exactly as you might expect: it goes as 1/r². There are a fixed number of photons, or quanta of light, that are emitted by a source, and the number of photons that you intercept determines the brightness you perceive. Even though our senses might be adapted to view brightnesses logarithmically, rather than according to this law, this is how the physical quantity of brightness behaves.

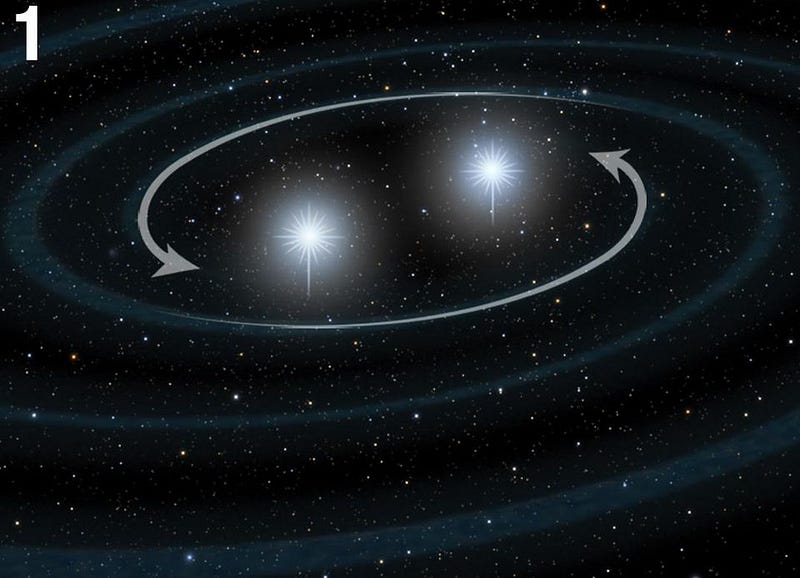
So you might expect that gravitational waves would behave the same way. When you have two masses orbiting one another, inspiraling, merging, or otherwise moving through a changing gravitational field, gravitational radiation (or gravitational waves) get created. Much like light, these waves spread out to cover all of space, exactly as you would expect for any form of radiation.

There’s a certain amount of energy that gravitational waves carry, and that energy is fixed as they travel through space. If you’re a specific distance away, you’ll perceive the strength of a gravitational wave to have a particular value.

But here’s the puzzle: if you ask how gravitational waves behave as a function of distance, the signal we see doesn’t behave as 1/r². Instead, it behaves simply as a 1/r law: inversely proportional to the distance alone. If you moved twice as far away from the source that emitted these waves, the signal would be half as strong, not a quarter as strong. If you moved ten times as distant as you were initially, the signal would be 10% of its original strength, not 1%.

You can immediately see the benefits in this: a signal remains much stronger if it obeys an inverse distance law, instead of an inverse distance-squared law. It gives us lots of hope for detecting ultra-distant gravitational waves, and it means if we can build a detector that’s 100 times as sensitive, we can see 100 times as far, rather than the 10 times as far we could see with a light detector that was 100 times as sensitive.

This is what happens, but describing the phenomenon doesn’t explain why it occurs like this. Sure, it’s great to be able to see so far, and to have an effect fall off more slowly with distance than you might have otherwise expected. It certainly increases your range, which seems vitally important when you consider that gravitational waves themselves are such weak signals to begin with.

But if you think about light — electromagnetic radiation — as a collection of particles that spreads out as you move away from a source, you can understand the brightness you receive as being related to the number of particles you collect with your telescope.

Why, then, wouldn’t you think of gravitational radiation as a collection of particles (gravitons, perhaps) that get emitted and spread out in the same fashion? Why wouldn’t it scale the same way as light?

First off, there are fundamental ways that light and gravitational waves are the same. They both:

• do carry energy,
• do reach infinite distances,
• do spread out over space (in roughly a sphere) as you move farther away,
• and will be detectable, at a certain distance, in proportion to the magnitude of the signal.

Because the geometry of space is the same for both light and gravitation, the difference between these two behaviors must lie in the nature of the signal that we can detect.

To understand that, we need to understand how gravity is a fundamentally different kind of force than electromagnetism. This will lead us to better understand how gravitational radiation (our gravitational waves) behave differently than electromagnetic radiation (light) when we allow it to propagate across the vast distances of intergalactic space.

If you want to create electromagnetic or gravitational radiation, how could you do it? The simplest way you could imagine — which (spoiler) doesn’t work — would be to spontaneously create or destroy charge in a region of space. Having a charge pop into (or out of) existence would create radiation of a very specific type: monopole radiation. Monopole radiation is what happens when you have a change in the amount of charge that’s present.

We cannot do this for either electromagnetism or gravitation, however. In electromagnetism, electric charge is conserved; in gravitation, mass/energy is conserved. The fact that we don’t get monopole radiation is important for the stability of our Universe. If charge or mass could spontaneously be created or destroyed, existence would be extremely different!

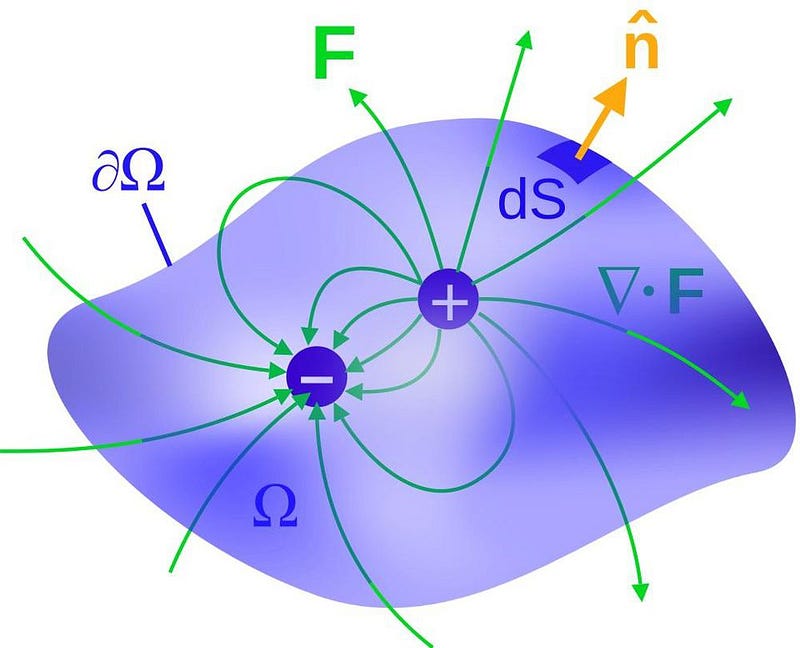
If charge and mass/energy are conserved, then the next step is to either move your charges (or masses) rapidly back-and-forth, or to take charges of opposite signs and change the distance between them. This would create what we call dipole radiation, which changes the distribution of charge without changing the total amount of charge.

In electromagnetism, this creates radiation, because moving an electric charge back-and-forth changes the electric and magnetic fields together. This matters, because changing electric and magnetic fields that are mutually perpendicular to each other and in-phase if wis what an electromagnetic wave actually is. This is the simplest way to make light, and it radiates just like you’re familiar with. The light carries energy, and the energy is what we detect, which is why objects appear dimmer as 1/r² the farther away they are.

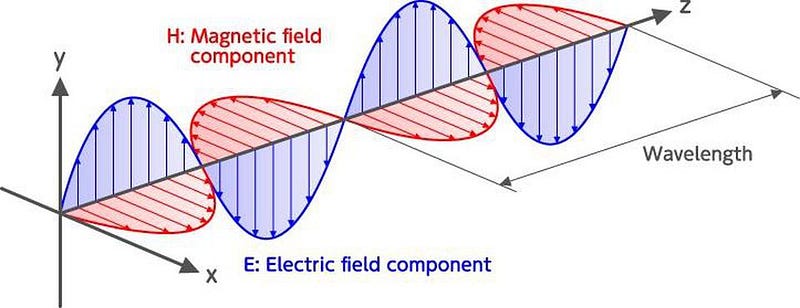
In gravity, however, freely moving a mass doesn’t make gravitational radiation, because there’s a conservation rule about masses in motion: the conservation of momentum. Similarly, separating masses doesn’t make gravitational radiation either, because the center of mass remains constant. There’s also a conservation rule about masses moving at a certain distance from the center of mass: the conservation of angular momentum.

Because energy, momentum, and angular momentum are conserved, you have to go past both monopole and dipole moments; you need a specific change in how the masses are distributed around their mutual center of mass. The simplest way to imagine this is to take two masses and have them mutually rotate around their center of mass, which results in what we call quadrupole radiation.

The amplitude of gravitational quadrupolar radiation falls off as 1/r, meaning the total energy falls off as 1/r², just as it did for electromagnetic radiation. But this is where the fundamental difference between gravitation and electromagnetism comes in. There’s a big difference between what you can physically detect for quadrupole and dipole radiation.

For electromagnetic (dipole) radiation, when the photons hit your detectors, they get absorbed, causing a change in the energy levels, and that change in energy — which remember, falls off as 1/r² — is the signal you observe. That’s why objects appear to dim according to an inverse square law.

For gravitational (quadrupole) radiation, however, it doesn’t get directly absorbed in a detector. Rather, it causes objects to move towards or apart from one another in proportion to the amplitude of the wave. Even though the energy falls off as 1/r², the amplitude only falls off as 1/r. That’s why gravitational waves fall off according to a different law than electromagnetic waves.

This is why we need to be so mind-bogglingly sensitive when we try to measure a gravitational wave. Even though they carry enormous amounts of energy, the amplitudes are exceptionally tiny. The first gravitational wave we ever detected, which was a binary black hole merger over a timespan of about 0.2 seconds, briefly emitted more energy than all the stars in the observable Universe combined.

But the amplitude, as we received it, compressed and expanded the entire Earth by about the diameter of three protons. The energy is huge and falls off as 1/r², but we cannot detect energy for gravitational waves. We can only detect amplitude, which (thankfully) only falls off as 1/r, which is a very good thing. The amplitudes may be tiny, but if we can detect any signal at all, it’s only a small step forward to detecting that same magnitude signal at any distance.

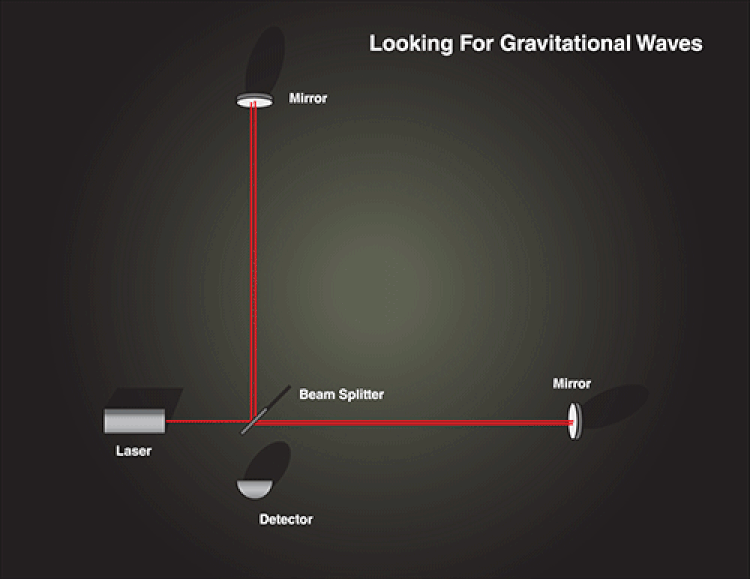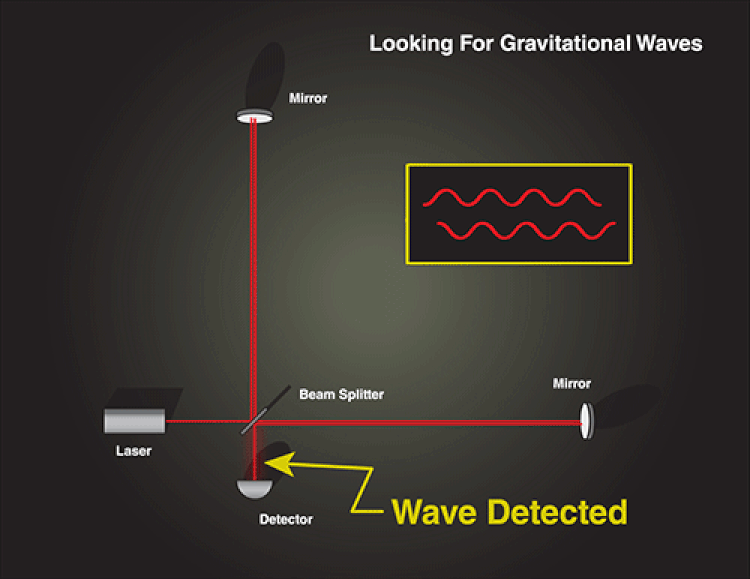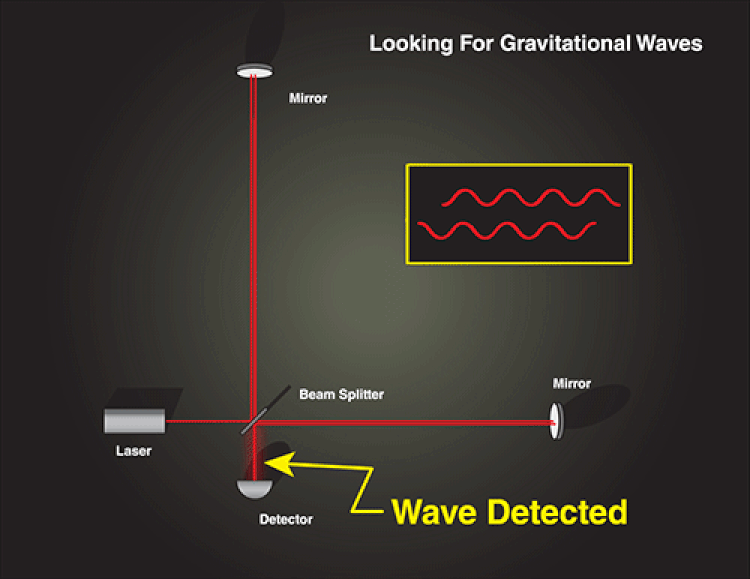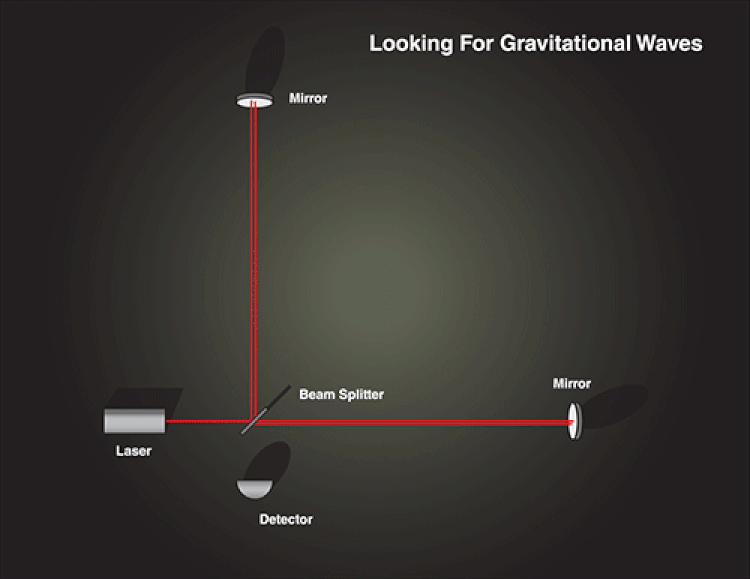
The future of gravitational wave astronomy is bright, as we can now see those tiny amplitudes. Even now, LIGO and Virgo are preparing for Run III, which will include a more sensitive noise floor. We expect this will reveal at least 1 new gravitational wave per week, and possibly as many new sources as one new detection per day.

But if we could somehow detect energy instead of amplitude, it would be a revolution. Even the weakest gravitational wave source we’ve seen, of the neutron star merger in 2017, carried more energy to us than the brightest star in the sky, Sirius, does in electromagnetic radiation.

Gravitational waves are a whole new type of astronomy, and it’s the amplitude that matters most of all for detection. The radiation may be fundamentally different in nature than the light we’re used to, but now that we’ve figured out how to observe it, there’s no going back. The Universe, in a whole new form of energy, is ours to explore.

Send in your Ask Ethan questions to startswithabang at gmail dot com!