Ask Ethan: Why Do Mirrors Flip Left-And-Right But Not Up-And-Down?


They don’t. If your mirror is on a horizontal surface, it does flip up-and-down! Here’s why.
If you’ve ever looked in a mirror, you’ve likely noticed that everything you see is flipped. When you raise your left hand, your reflection raises their right hand. When you wink with your right eye, your reflection’s left eye winks back. And if you write a message and hold it up, you’ll see your reflection hold up the identical sign, but everything appear backwards, even the individual letters themselves. It appears that everything you see reflected in the mirror has their left-and-right reversed. But, for some reason, up-and-down don’t appear to be reversed. Your mirror reflection still has their feet on the ground, their ceiling up above, and all the letters on your mirror image’s writings aren’t flipped upside down, but remain right side up. Why is that? That’s what Matt Foley wants to know, writing in to ask:
“It’s well known that mirrors exchange left and right. Why don’t they exchange up and down? If we lived in a zero-gravity environment, how would our perceptions differ? If we were a sea star with five equal axes of symmetry, how would we conceive of the situation?”
Whether you were a sea star, an insect, a jellyfish, a parakeet or a human — whether you were in space or on Earth or anywhere else in the Universe — you’d still see the same thing. Mirrors appear to reverse left-and-right, but not up-and-down. Here’s why.

The first thing you have to recognize is there’s nothing special about our environment here. There’s nothing remarkable, as far as mirrors and reflections go, about:
- our human eyes,
- our planet Earth,
- our gravitationally-based orientation of up-and-down,
- or the nature of light,
that has any effect on the outcome.
We could turn gravity on or off; we could rotate ourselves by any angle, even 45°, 90°, or 180° about any axis; we could give ourselves additional eyes or senses; we could rearrange the objects surrounding us in any configuration we like. Still, despite any of these modifications, we’d still see that up remained up, down remained down, and that everything in the mirror would appear as though left and right were switched.
One of the best examples to illustrate this is to consider a spinning ball in the mirror, and to consider it from two perspectives: one of a ball spinning about its vertical axis, like a basketball on an adept athlete’s finger, and one of a ball spinning about its horizontal axis instead.

When you spin a ball about its vertical axis, you can consider the fact that there are two ways to do it. Either, if you looked “down” at this ball from above, you’d see that it appeared to spin clockwise, from ahead to the right to behind to the left to ahead again, or counterclockwise, in the exact opposite direction.
If the ball is spinning clockwise, you can model that with your left hand. If you take your left hand and point your thumb up, you’ll notice that your fingers curl around in the clockwise direction. A clockwise-spinning ball follows this exact same orientation.
But now, take a look at the ball — and your left hand’s — reflection in the mirror. If you were to look “down” at that ball once again, from above, you’d see that it was rotating counterclockwise instead. If you followed the point on the ball that began closest to you, you’d see it move to your right and backwards, away from you, then farther away and back to the center, then closer and towards the left, then closer still and back to the center. That counterclockwise motion could be described by your own right hand, showing how, once again, the mirror appeared to exchange left-for-right, while leaving the up-and-down direction unchanged.

What about if we then switched to spinning a ball about its horizontal axis? How would a mirror handle that?
Imagine that you’re holding the ball in front of you so that it’s sandwiched between your two index fingers that are pointing towards one another. We again have two choices of how to rotate it, so let’s pick one: overhand and away from you. If we start at the point on the ball closest to your body’s core, you’ll see it move:
- up and away from you,
- then back down towards the middle but still away from you,
- then further down away from the middle and back towards you,
- and then back up towards the middle and towards you,
whereupon it returns to its initial position. This “underhand” rotation was one choice you could have made; the reverse of it would lead to an “overhand” rotation instead. (If you’ve ever been part of an argument on which way is the “proper” way to hang a toilet paper roll, you’ll recognize these two visualizations.)
But this time, when you look in the mirror, what’s happening? Left and right are the same. Up and down are the same. But the ball? The mirrored version of the ball, instead of appearing to spin with an underhand rotation, appears to be spinning with an overhand orientation.

This example surprises most people. Sure, it’s clearly symmetric about the vertical axis; if you were to draw an imaginary line down your center, with the ball rotating about its horizontal axis, it’s clear that the left half of yourself and the right half are completely symmetric. Same with your reflection in the mirror: left and right appear completely symmetric.
Sure, your mirror is still replacing your left with your right. Your reflection’s right hand corresponds to your left hand; your reflection’s left hand corresponds to your right. From the perspective of your reflection, their ball is doing the same thing that your ball is from your own perspective, moving up and away from their body, then down and away, then down and towards, and then up and towards, returning to its initial position.
But if they see their ball spinning “underhand” from their perspective, yours appears to spin “overhand” from their perspective. The mirror appears to be flipping the rotational direction of that ball as well.

There’s a very powerful clue as to what’s going on with mirrors from this example, if we’re clever enough to identify it. Imagine — and we can imagine anything we like in this example — that the ball that’s spinning about its horizontal axis is now transparent. What we’re going to do is to create a single point on this ball, right along its equator, that we can track, as though we took a permanent marker and drew a point on a ball that was made of clear glass.
Now, from our perspective in the real Universe, we’re going to track the position of both our dot and the dot that appears in the mirror. Simultaneously, starting with the dot positioned closest to our own body, what we see is as follows:
- the real dot begins closest to us and farthest from the mirror, and so the mirrored dot begins farthest from us from our perspective,
- then the real dot rises up and gets farther away from us but closer to the mirror, whereas the mirrored dot rises up and gets closer to us,
- then, after reaching its maximum height, the real dot descends while reaching its most distant point from us but closest to the mirror, while the mirrored dot similarly descends while reaching its closest point to us,
- then the real dot starts to return closer to us while it descends, moving farther from the mirror, while the mirrored dot continues its descent and moves back away from us,
- and then the real dot, after reaching its minimum elevation, rises once again, getting closer to us (and farther from the mirror) until it returns to its original position, while the mirrored dot rises similarly, retreating farther from us and farther from the mirror until it returns to its initial position as well.
Left and right, as you can see, play absolutely no role in this example. We’re just looking at a single point that moves up-and-down while also moving forward-and-backwards. When the real dot appears to move up, the mirrored dot appears to move up. When the real dot appears to move down, the mirrored dot appears to move down. There is no flipping of up-and-down here.
But there isn’t a flipping of left-and-right, either!
If you were to perform the same experiment with a clear glass ball and a drawn-on dot, but rotated the ball around its vertical axis instead of its horizontal axis, you’d notice that:
- when your dot moved to the left, the mirrored dot moves to the left,
- when your dot moved back to the center, the mirrored dot moves to the center,
- when your dot moved to the right, the mirrored dot moves to the right,
- and when your dot returns to the center, the mirrored dot also returns to the center.
Something is happening, clearly, but it isn’t that left-to-right is getting reflected, either.

And yet, mirrors really are reflective surfaces. They don’t switch up-and-down but they also don’t switch left-and-right. Instead, what mirrors do is they reflect back-to-front: the third (depth) dimension!
Think about what happens when you look at yourself in the mirror. Light — even though it’s ambient light reflected off your body from elsewhere in the room — comes from every part of you. There’s no perspective from which you’re invisible, and hence that light must be radiating outwards in all directions.
The only way you can ever see anything is if light enters your eyes, just like the only way a camera, telescope, or other observer can see anything is if photons (or light rays) interact with it at a particular location: a specific time and place. So if we want to know what you’re going to see and where you’re going to see it, all you need to do is trace out the light rays: from whatever part of your body they’re emitted from, reflected off the mirror (obeying the physical laws that govern optics), and ending at your eyes. Based on the total distance the light travels and the angle it comes in at, that’s where your eyes and brain infer the “image” in the mirror to be.

If your body were partially transparent, allowing you to see inside your reflection’s body, you’d find that everything was flipped front-to-back. Your left hand, when you hold it up, appears as though your fingernails are closer to you, your palm is farthest from you, your thumb is on the right, and your fingers are pointing up. That’s what a left hand looks like.
But in the mirror, that same hand has its fingernails farthest from you, its palm is closest to you, its thumb is on the right, and its fingers are pointing up. That’s exactly what you’d see if you held your (real) right hand up but with your palm facing your face instead. In the mirror:
- a left hand becomes a right hand,
- writing gets flipped to be “mirrored” writing,
- objects that spin clockwise appear to spin counterclockwise,
- and vice versa on everything above.
But the reason is not because mirrors flip things left-to-right; they don’t. Instead, they flip things front to back, and that’s the explanation for what we see.

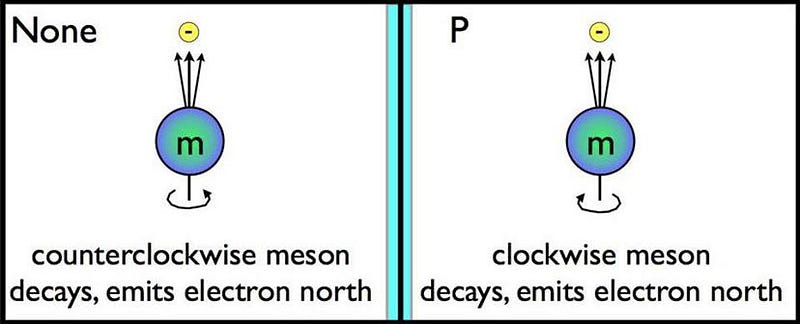
In physics, there’s a special type of symmetry that exists if what happens in the mirror is indistinguishable from what happens in reality: parity symmetry. Most of the laws of physics respect this symmetry, but not all of them. In particular, whenever you have a radioactive decay, you’re at risk of violating this symmetry, since particles have a spin, a spin axis, and a decay direction, the same way your hands have a direction that your fingers curl and and a direction that your thumb points. Right hands and left hands are fundamentally different — just like chiral molecules are different from one another — and so are spinning particles that have a decay direction. For those that do, parity is violated, the same way a right-handed person’s reflection appears to be left-handed instead.
What’s remarkable about the way mirrors work is that they’re completely independent of the observer. If our eyes were separated in the vertical direction rather than the horizontal direction, mirrors would still reflect front-to-back. If we were in zero-gravity, if we had only one eye, if we were a rotationally symmetric starfish, etc., it wouldn’t change what we see in the mirror at all. The only difference is that things are reflected front-to-back, and that changes the “handedness” of everything that appears in the mirror, irrespective of how we view it.
Send in your Ask Ethan questions to startswithabang at gmail dot com!
Starts With A Bang is written by Ethan Siegel, Ph.D., author of Beyond The Galaxy, and Treknology: The Science of Star Trek from Tricorders to Warp Drive.