Ask Ethan: What’s the deal with the speed of light?

Three simple questions; an amazing story that goes way beyond Einstein!

“Each ray of light moves in the coordinate system ‘at rest’ with the definite, constant velocity V independent of whether this ray of light is emitted by a body at rest or a body in motion.” –Albert Einstein, 1905

Nothing in the Universe can move faster than the speed of light in vacuum. 299,792,458 meters per second. If you’re a massive particle, you can only approach — but never reach — that speed; if you’re a massless particle, you are compelled to always travel at exactly that speed so long as you’re traveling through empty space. But how do we know that this is so, and what causes it? That what this week’s Ask Ethan question is about owing to Michael Carston, who has three simple questions about the speed of light:

Why is the speed of light finite? Why is the speed of light what it is? Why is not faster or slower?

Up until the 19th century, we didn’t know that any of this was even true.

When you pass light through water, a prism or any medium, it separates into its various colors. Reds bend at different angles from blues, creating phenomena like rainbows. Even outside of the visible spectrum, this is seen; infrared and ultraviolet light exhibit this same property. This is only possible if the speed of light in a medium is different for light of different wavelengths/energies. But in a vacuum, outside of any media, all light travels at the same finite speed.

This wasn’t realized until the mid-1800s, when the physicist James Clerk Maxwell showed what light truly is: an electromagnetic wave. Maxwell, for the first time, put the independent phenomena of electrostatics (stationary charges), electrodynamics (moving charges and currents), magnetostatics (constant magnetic fields) and magnetodynamics (induced currents and changing magnetic fields) into a single, unified framework. The equations that govern them — Maxwell’s equations — allowed you to calculate a very simple-sounding scenario: what types of electric and magnetic fields and properties can exist in empty space with no electric or magnetic sources? With no charges or currents, you might think you’d get nothing at all, but Maxwell’s equations surprisingly proved otherwise.

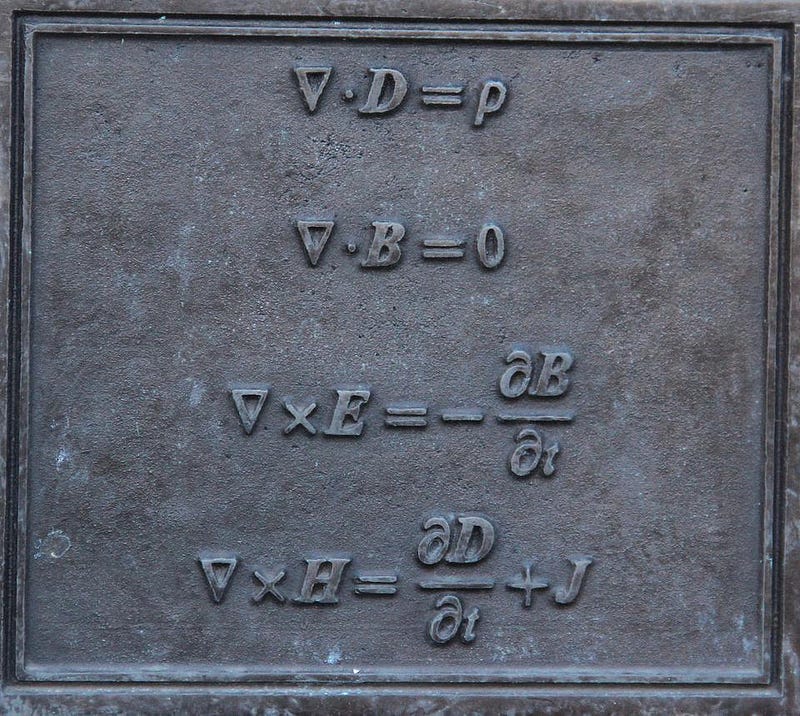
Nothing is one possible solution, but also possible are oscillating, in-phase, mutually perpendicular electric-and-magnetic fields. They have specific, well-defined amplitudes. they have energies defined by the frequency of oscillation of those fields. And they move at a very specific speed that is defined by two constants: ε_0 and µ_0, the two constants that define the magnitudes of the electric and magnetic forces in this Universe, respectively. The equation you get out is of a specific form: a wave. And like all waves, it has a speed: 1/√(ε_0 µ_0), which happens to be c, the speed of light in a vacuum.

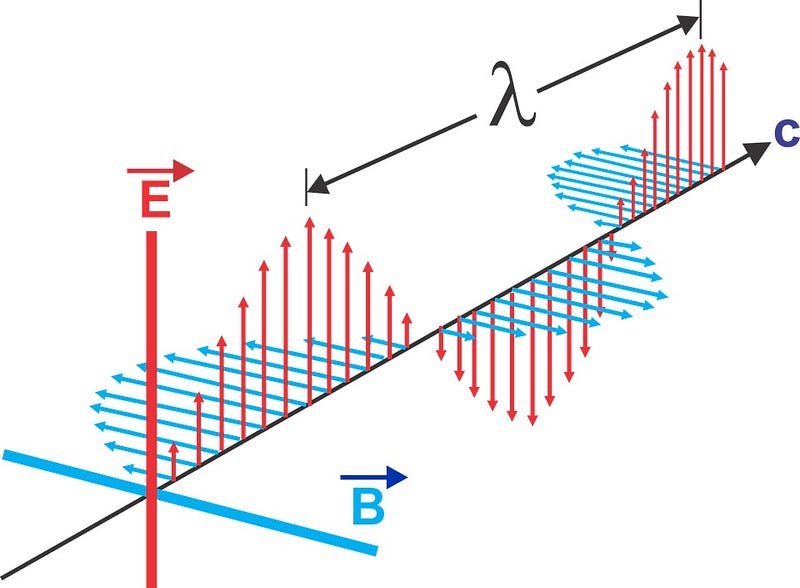
From a theoretical perspective, light is simply massless electromagnetic radiation. Because of what the laws of electromagnetism dictate, it must move at the speed of light — 1/√(ε_0 µ_0), or c — regardless of what its other intrinsic (energy, momentum, wavelength) properties are. ε_0 can be measured by building and measuring a capacitor; µ_0 is defined exactly from the Ampere, the unit of electric current, leading to c. That same fundamental constant, first derived by Maxwell in 1865, has since shown up in many other places:

• It’s the speed of any massless particle or wave, including gravitational waves.
• It’s the fundamental constant that relates your motion through space to your motion through time in relativity.
• And it’s the fundamental constant that relates energy to rest mass in the equation, E = mc².

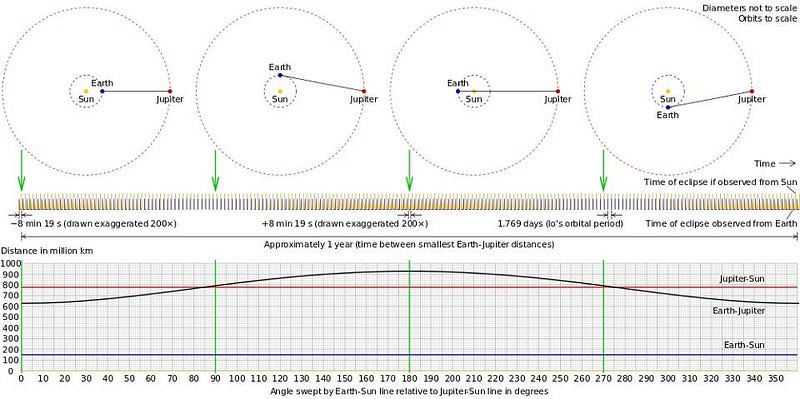
The first measurements of this actual value came from astronomical observations. When Jupiter’s moons slide in-and-out of eclipse, they appear ‘visible’ or invisible in particular patterns/orientations as visible from Earth in a way that’s dependent on the speed of light. That led to the first quantitative measurement of c, in the 17th century, which was then 2.2 × 10⁸ m/s. The aberration of starlight — from the motion of a star and of the Earth that the telescope is mounted to — can also be quantified. In 1729, this method was used to measure c to within 1.4% of its present value. By the 1970s, c had been measured to be 299,792,458 m/s with an uncertainty of less than 0.0000002%, with most of the uncertainty due to the difficulty of defining a perfectly accurate secondor meter. In 1983, the second and meter were both redefined in terms of c and the universal properties of atomic radiation. The speed of light, therefore, is now exactly 299,792,458 m/s.

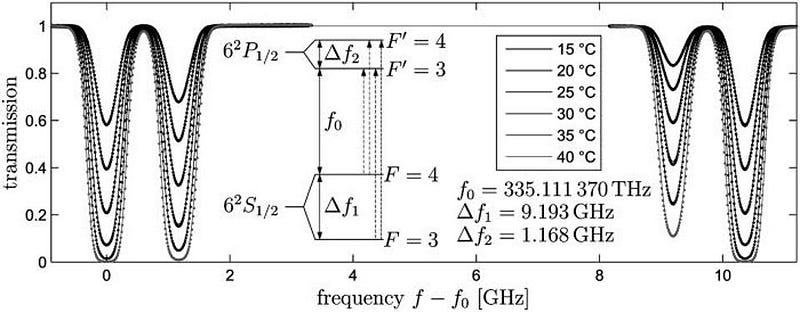
So why isn’t the speed of light faster or slower than that value? It’s as simple as the atom above. Atomic transitions occur as they do because of fundamental quantum properties given to the building blocks of nature. The interactions of an atomic nucleus with the electric and magnetic fields generated by the electrons and the rest of the atom cause some different energy levels to be extremely close to one another but slightly different: a phenomenon known as hyperfine splitting. In particular, the hyperfine structure transition frequency of caesium-133 atoms results in light of a very specific wavelength. When exactly 9,192,631,770 cycles of that light has passed, that time defines one second; the distance that light has traveled defines exactly 299,792,458 meters; the speed at which that light travels defines c.

It would take something to be fundamentally different about the nature of that transition or the light coming from it to change the definition. It also teaches us something incredibly valuable: seeing if atomic physics and atomic transitions worked differently at earlier times or at great distances would be evidence for the speed of light changing over time. So far, all the measurements we’ve made only place constraints on how constant the speed of light has always been, and the constraints are very good: less than 7% of a change in the present value over the past 13.7 billion years. If the speed of light were shown to be non-constant across any of these metrics, or different among different types of light, it would lead to the biggest physics revolution since Einstein. Instead, the evidence we have points to a Universe where the laws of physics have always been the same, at all locations, in all directions and at all times, including the physics of light itself. In its own way, that’s pretty revolutionary, too.

Submit your Ask Ethan questions and suggestions to startswithabang at gmail dot com.

This post first appeared at Forbes, and is brought to you ad-free by our Patreon supporters. Comment on our forum, & buy our first book: Beyond The Galaxy!