Ask Ethan: How Do Quantum Fields Create Particles?

If everything in nature is made of quantum fields at its core, how do we wind up with particles at all?

What is our Universe made out of? At a fundamental level, to the best of our knowledge, the answer is simple: particles and fields. The type of matter that makes up humans, Earth, and all the stars, for example, is all composed of the known particles of the Standard Model. Dark matter is theorized to be a particle, while dark energy is theorized to be a field inherent to space itself. But all the particles that exist, at the core of their nature, are just excited quantum fields themselves. What gives them the properties that they have? That’s the topic of this week’s question, coming to us from Richard Hunt, who wants to know:

I have a question about Quantum fields. If we model particle properties as excitations of various independent fields (Higgs field for mass, EM field for charge etc) then what causes these excitation waves to travel around together? Is there really some kind of particle entity underlying these waves?

In other words: what makes a particle have the properties that it does? Let’s take a deep look.

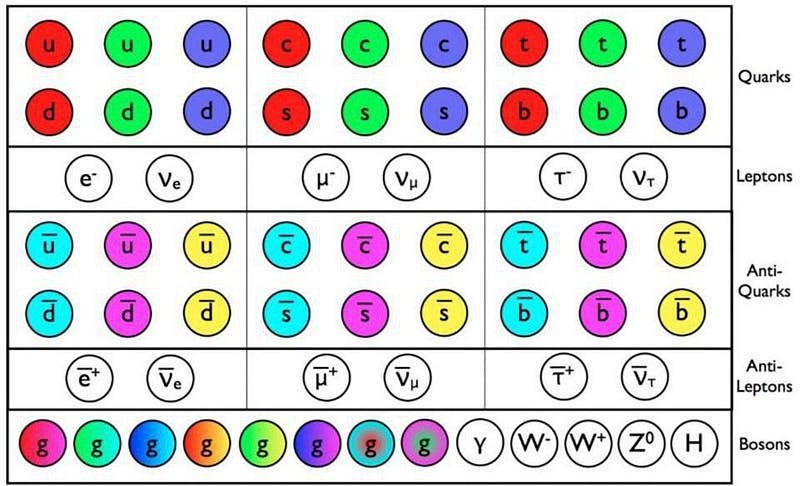
The particles that we know of have traits that appear to be inherent to them. All particles of the same type — electrons, muons, up quarks, Z-bosons, etc. — are, at some level, indistinguishable from one another. They all have a slew of properties that all other particles of the same type share, including:

• mass,
• electric charge,
• weak hypercharge,
• spin (inherent angular momentum),
• color charge,
• baryon number,
• lepton number,
• lepton family number,

and more. Some particles have a value of zero for many of these quantities; others have non-zero values for almost all of them. But somehow, every particle that exists contains all of these particular, intrinsic properties bound together in a single, stable, “quantum state” we call a particular particle.

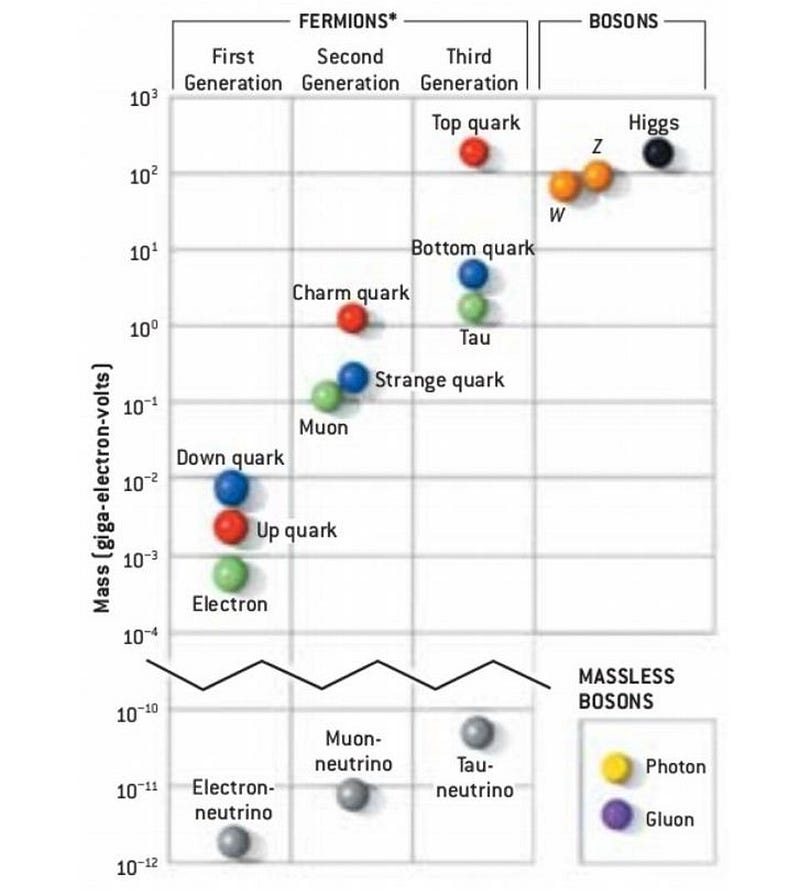
Underlying all of it, there are a variety of fields that exist in the Universe. There’s the Higgs field, for example, which is a quantum field that permeates all of space. The Higgs is a relatively simple example of a field, even though the particle that arose from its behavior — the Higgs boson — was the last one ever to be discovered. The electromagnetic (QED) field and color-charge (QCD) field, among others, are also fundamental quantum fields.

Here’s how it works: the field exists everywhere in space, even when there are no particles present. The field is quantum in nature, which means it has a lowest-energy state that we call the zero-point energy, whose value may or may not be zero. Across different locations in space and time, the value of the field fluctuates, just like all quantum fields do. The quantum Universe, to the best of our understanding, has rules governing its fundamental indeterminism.

So if everything is fields, then what is a particle? You may have heard a phrase before: that particles are excitations of quantum fields. In other words, these are quantum fields not in their lowest-energy — or zero-point — state, but in some higher-energy state. But exactly how this works is a bit tricky.

Up until this point, we’ve been thinking of fields in terms of empty space: the quantum fields we’re discussing exist everywhere. But particles don’t exist everywhere at once. On the contrary, they’re what we call localized, or confined to a particular region of space.

The simplest way to visualize this is to impose some sort of boundary conditions: some region of space that can be different from purely empty space.

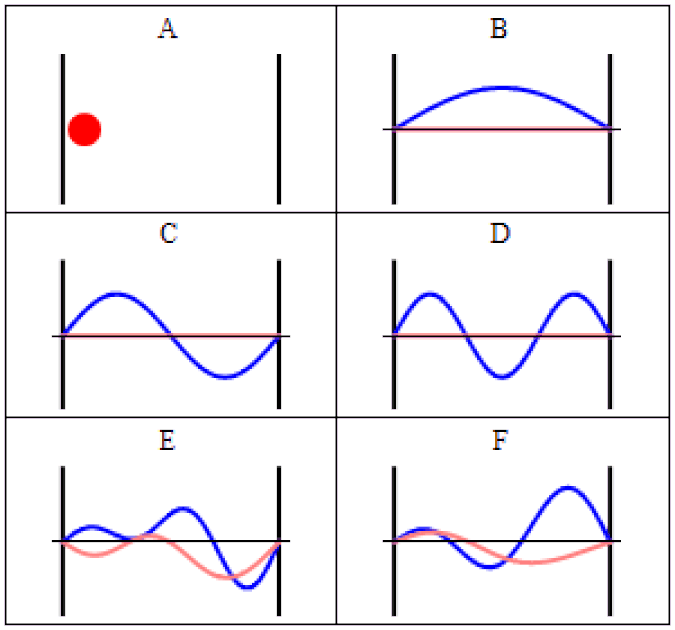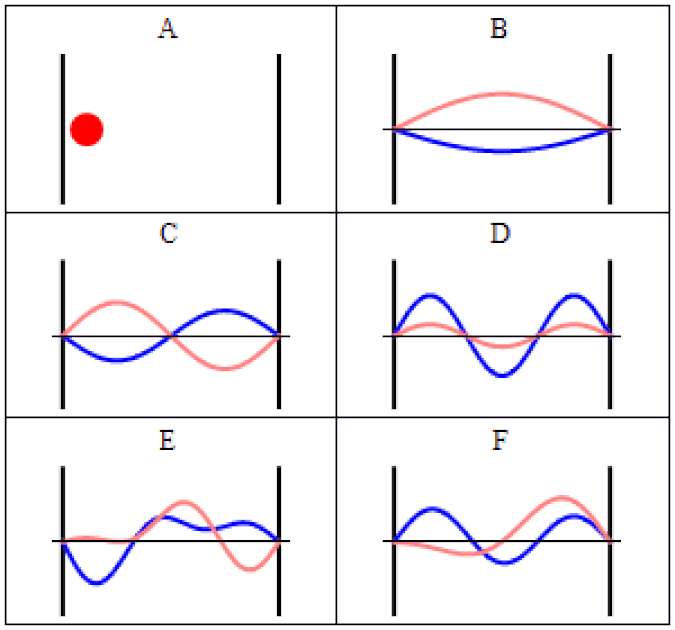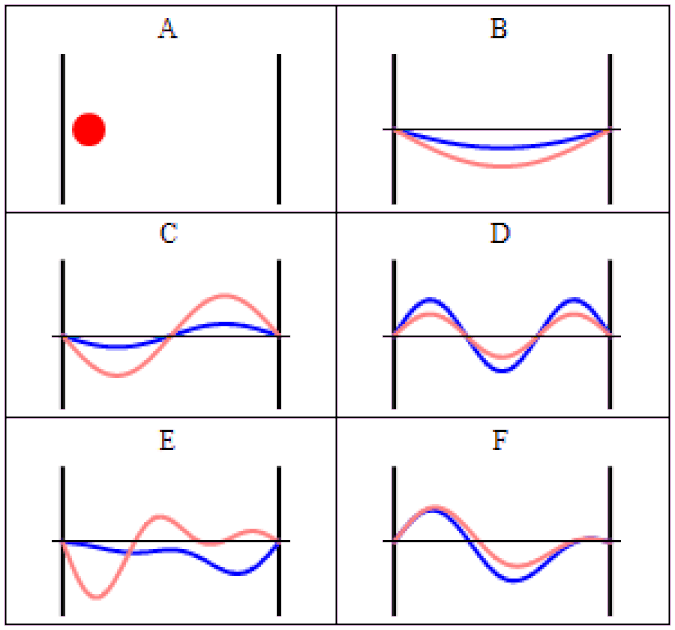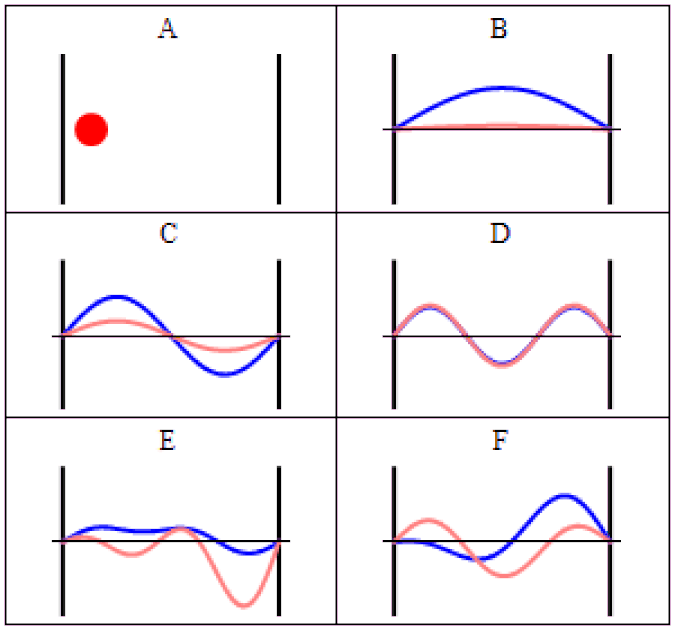
In our pre-quantum picture of the Universe, particles are simply points and nothing more: individual entities with a set of properties assigned to them. But we know that in the quantum Universe, we have to replace particles with wavefunctions, which are a probabilistic set of parameters that replace classical quantities like “position” or “momentum.”

Instead of unique values, there are a set of possible values that a quantum field can take on. Some of the properties associated with a particle are continuous, like position, while others are discrete. The discrete ones are the most interesting in terms of fundamental particle properties, since those can only take on specific values that are defined by the characteristic conditions that the Universe sets out.

A simple way to visualize this is to imagine a guitar. On a guitar, you have six strings of different thicknesses, where we can view thickness as a fundamental property of the string. If all you had were these strings (and no guitar), and you asked the question of the number of different possible ways these strings could vibrate, you’d wind up with an infinite number of allowable outcomes.

But guitars don’t offer an infinite set of possibilities at all. We have boundary conditions on those strings:

• the effective length of each string is constrained by the start-and-end points,
• the number of possible excitations are constrained by the positions of the frets on the fretboard,
• the vibrational modes are constrained by geometry and the music of overtones,
• and the possible sounds it can make are constrained by the tension of each string.

These properties are uniquely determined by the size, string properties, and tuning of each individual guitar.

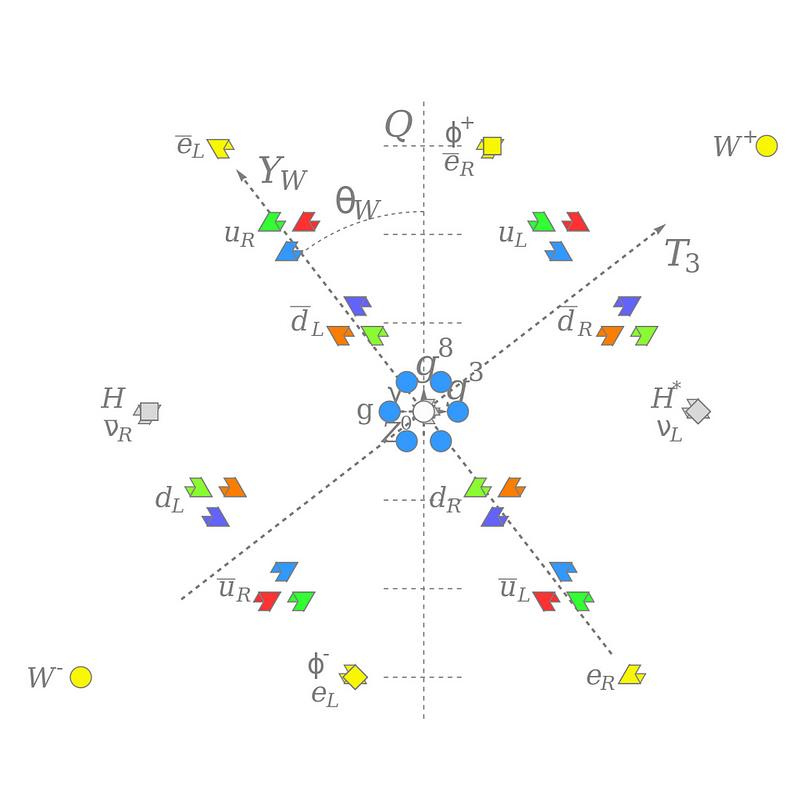
In the case of our Standard Model particles, there are also a finite set of possibilities. They arise from a specific type of quantum field theory: a gauge theory. Gauge theories are invariant under a slew of transformations (like speed boosts, position translations, etc.) that our physical laws should also be invariant under.

The Standard Model in particular comes from a quantum field theory made up of three groups (as in the mathematics of Lie groups) all tied together:

• SU(3), a group that’s made of 3 × 3 matrices, which describes the strong interaction,
• SU(2), a group that’s made of 2 × 2 matrices, which describes the weak interaction,
• and U(1), known as the circle group and made of all complex numbers with an absolute value of 1, which describes the electromagnetic interaction.

Put these all together in the proper way — SU(3) × SU(2) × U(1) — and you get our Standard Model.

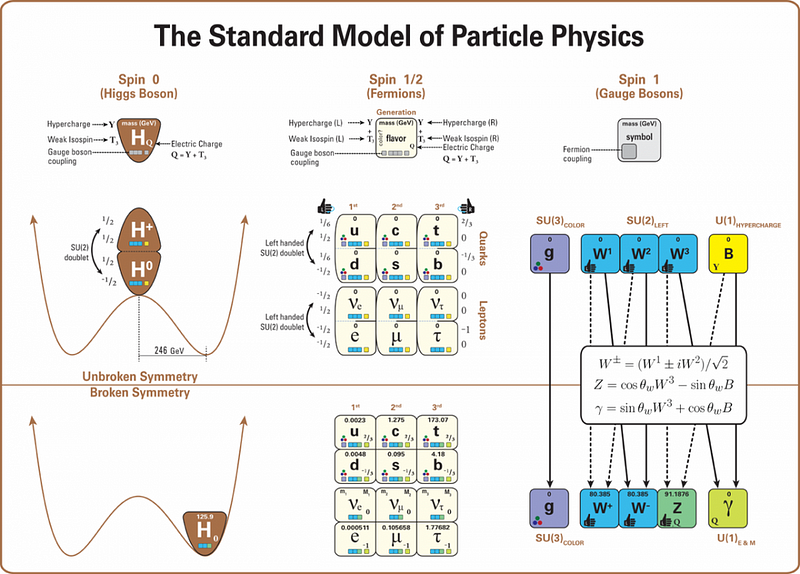
The Standard Model isn’t just a set of laws of physics, but provides proverbial boundary conditions that describe the spectrum of particles that can exist. Because the Standard Model isn’t just made of a single quantum field in isolation, but all of the fundamental ones (except gravity) working together, the spectrum of particles we wind up with has a fixed set of properties.

This is determined by the specific mathematical structure — SU(3) × SU(2) × U(1) — that underlies the Standard Model. Each particle corresponds to the fundamental quantum fields of the Universe all excited in a particular way, with explicit couplings to the full suite of fields. This determines their particle properties, like:

• mass,
• electric charge,
• color charge,
• weak hypercharge,
• lepton number,
• baryon number,
• lepton family number,
• and spin.

If the Standard Model were all there were, no other combinations would be allowed. The Standard Model gives you fermion fields, which correspond to the matter particles (quarks and leptons), as well as boson fields, which correspond to the force-carrying particles (gluons, weak bosons, and photon), as well as the Higgs.

The Standard Model was built with a set of symmetries in mind, and the particular ways these symmetries break determine the spectrum of allowed particles. They still require us to put in the fundamental constants that determine the specific values of particle properties, but the generic properties of a theory with:

• 6 quarks and antiquarks with three colors each,
• 3 charged leptons and antileptons,
• 3 neutrinos and antineutrinos,
• 8 massless gluons,
• 3 weak bosons,
• 1 massless photon,
• and 1 Higgs boson,

are determined by the Standard Model itself.

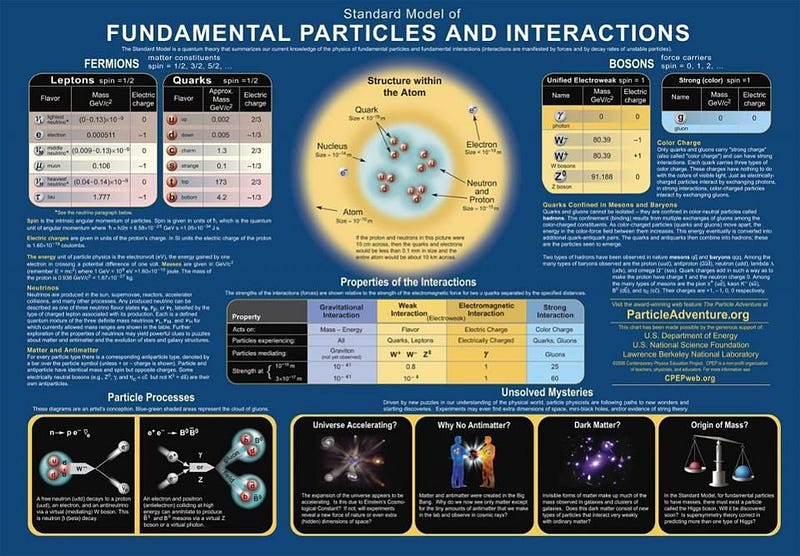
So how do we get quantum particles with the properties we do? Three things come together:

1. We have the laws of quantum field theory, which describe the fields permeating all of space that can be excited to different characteristic states.
2. We have the mathematical structure of the Standard Model, which dictates the allowable combinations of field configurations (i.e., particles) that can exist.
3. We have the fundamental constants, which provide the values of specific properties to each allowable combination: the properties of each particle.

And there may be more. The Standard Model may describe reality extremely well, but it doesn’t include everything. It doesn’t account for dark matter. Or dark energy. Or the origin of the matter-antimatter asymmetry. Or the reasons behind the values of our fundamental constants.

The Standard Model only provides the allowable configurations we know of. If neutrinos and dark matter are any indication, there ought to be more. One of the prime goals of 21st century science is to find out what else is there. Welcome to the cutting-edge frontier of modern physics.

Send in your Ask Ethan questions to startswithabang at gmail dot com!