Ask Ethan: How Do Black Holes Really Evaporate?

Hawking’s greatest achievement is also the greatest source of misunderstanding.

“Maybe that is our mistake: maybe there are no particle positions and velocities, but only waves. It is just that we try to fit the waves to our preconceived ideas of positions and velocities. The resulting mismatch is the cause of the apparent unpredictability.” –Stephen Hawking

Perhaps the greatest thing Stephen Hawking ever discovered — and the reason he’s so renowned among physicists — is that black holes don’t live forever.

Rather, they radiate their energy away over extraordinarily long timescales through a process discovered in 1974 that’s now known as Hawking radiation. The big question for this week, that Spencer Müller Diniz wants to know the answer to, is:

Ever since Stephen Hawking discovered Hawking Radiation, scientific publications describe it as a phenomenon where black holes slowly “evaporate” due to spontaneous creation of quantum entangled particle pairs near the event horizon. It is said the one of the particles gets sucked in to the black hole and the other escapes as Hawking [Radiation.] Because of Hawking Radiation, black holes slowly lose mass until eventually evaporating completely. The question is, if one particle falls in the black hole and the other is ejected, why is the black hole getting smaller? Shouldn’t it actually be gaining mass?

This is a big question, and it’s one that’s loaded with misconceptions, many of which are Stephen Hawking’s own fault. So let’s get into it!

This month marks the 100th anniversary of the very first exact solution ever discovered in General Relativity: the spacetime that describes a massive singularity with an event horizon around it. The discovery was made by Karl Schwarzschild, who immediately realized that this would be a black hole: an object so massive and dense that nothing, not even light itself, could escape from its gravitational pull.

For a long time, it was recognized that if you got enough mass together in a small enough region of space, gravitational collapse down to a black hole would be inevitable, and that no matter what the original configuration of the mass was, the singularity would be a point, and the event horizon would be a sphere. In fact, the only parameter of interest — the size of that event horizon — was determined exclusively by the black hole’s mass.

As the black hole swallowed more and more matter over time, its mass would grow, and hence it would increase in size. For a long time, it was thought that this would continue without fail, until there was no more matter left to swallow or the Universe came to an end.

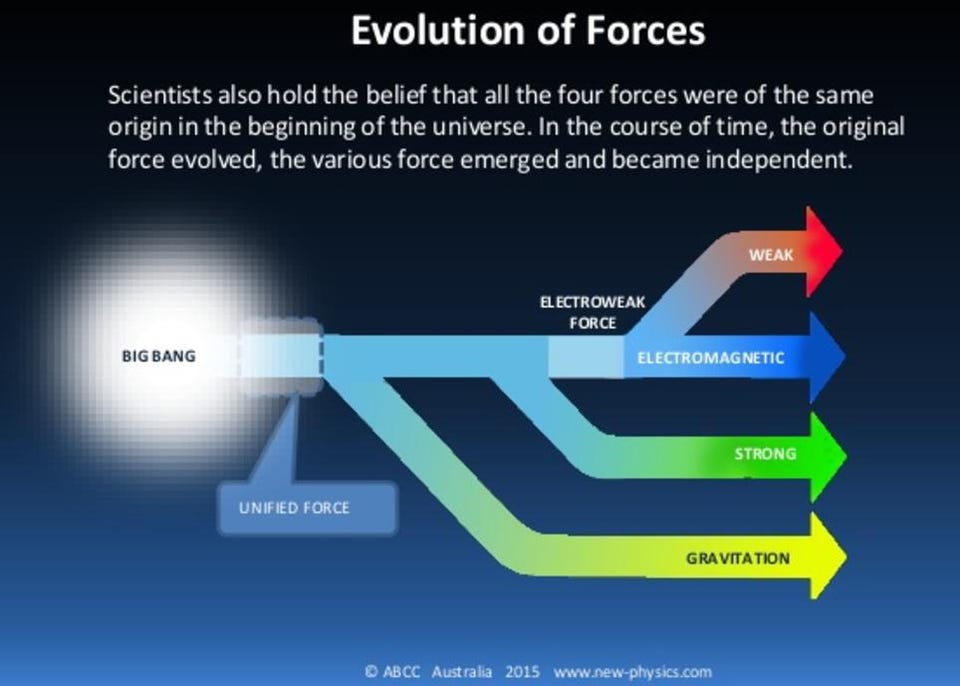
But something happened to change this picture: the revolution that our Universe was made up of tiny, indivisible particles that obeyed a different set of laws, quantum laws. Particles interacted with one another through a variety of fundamental interactions, each of which could be expressed as a set of quantum fields.

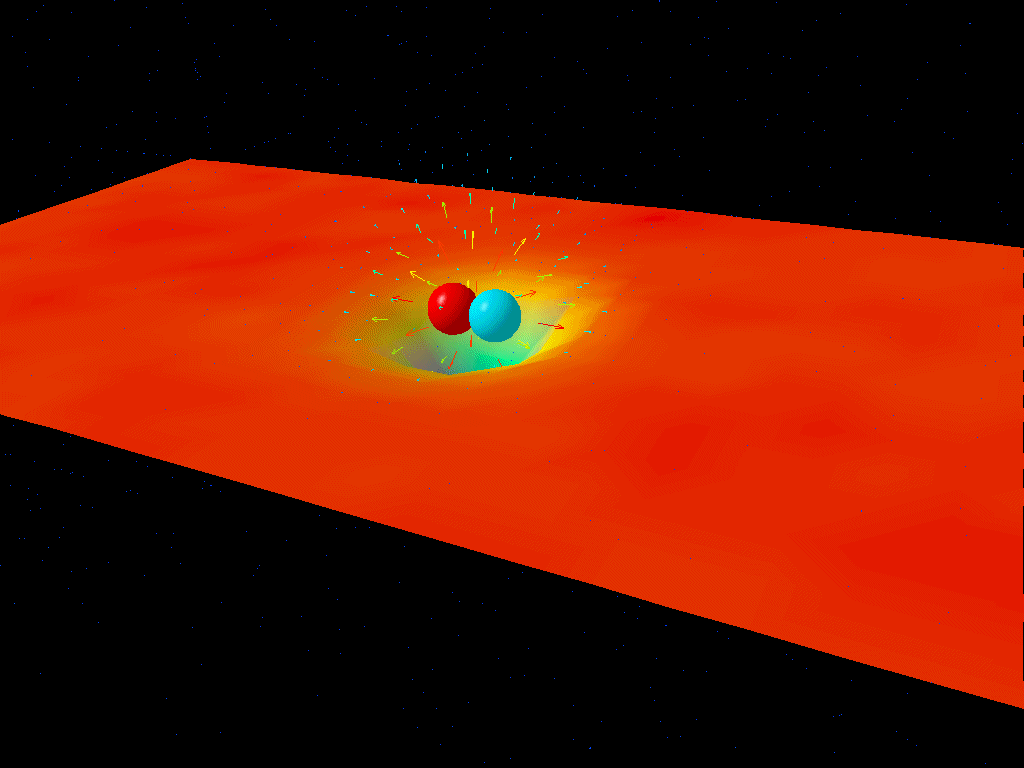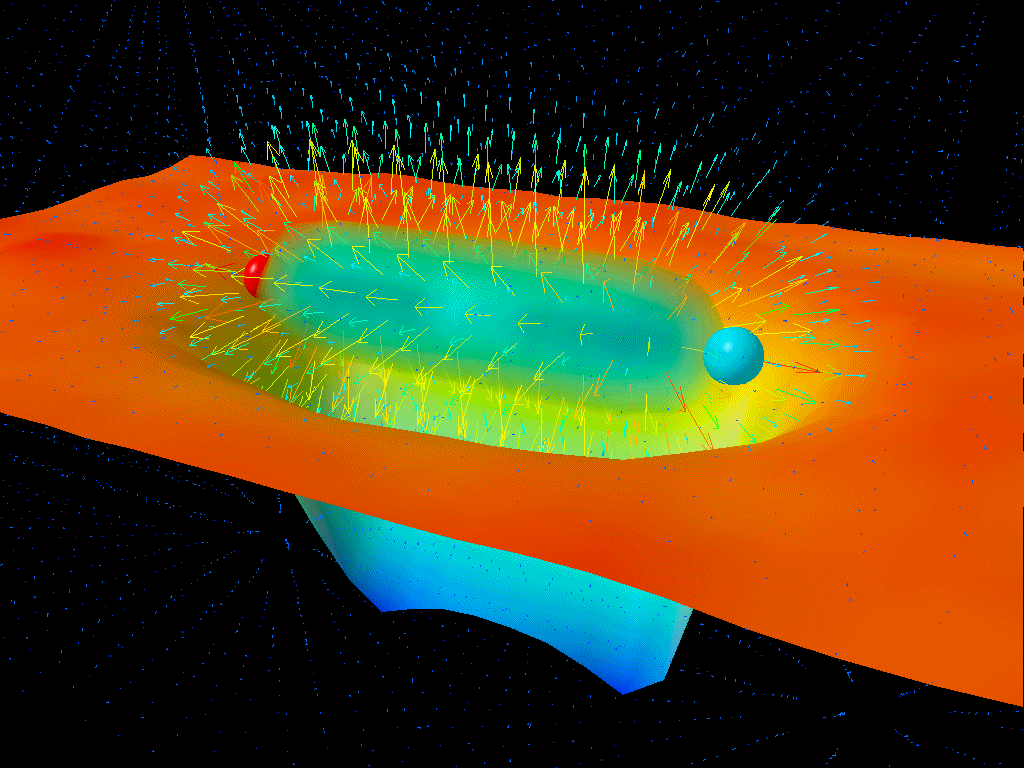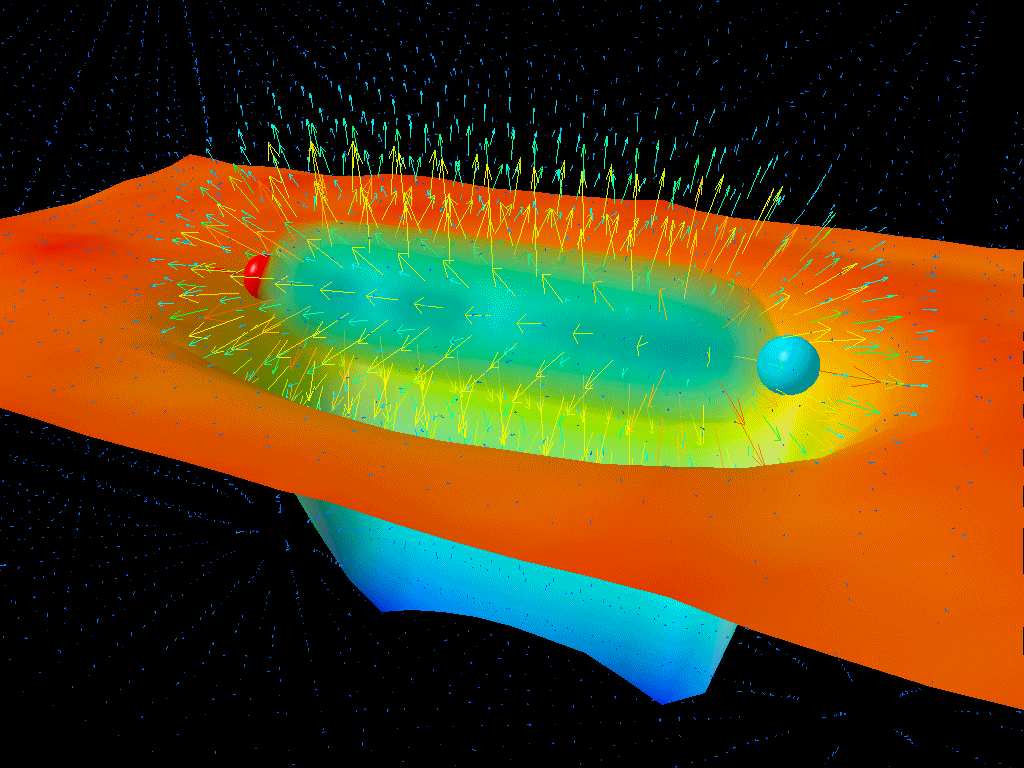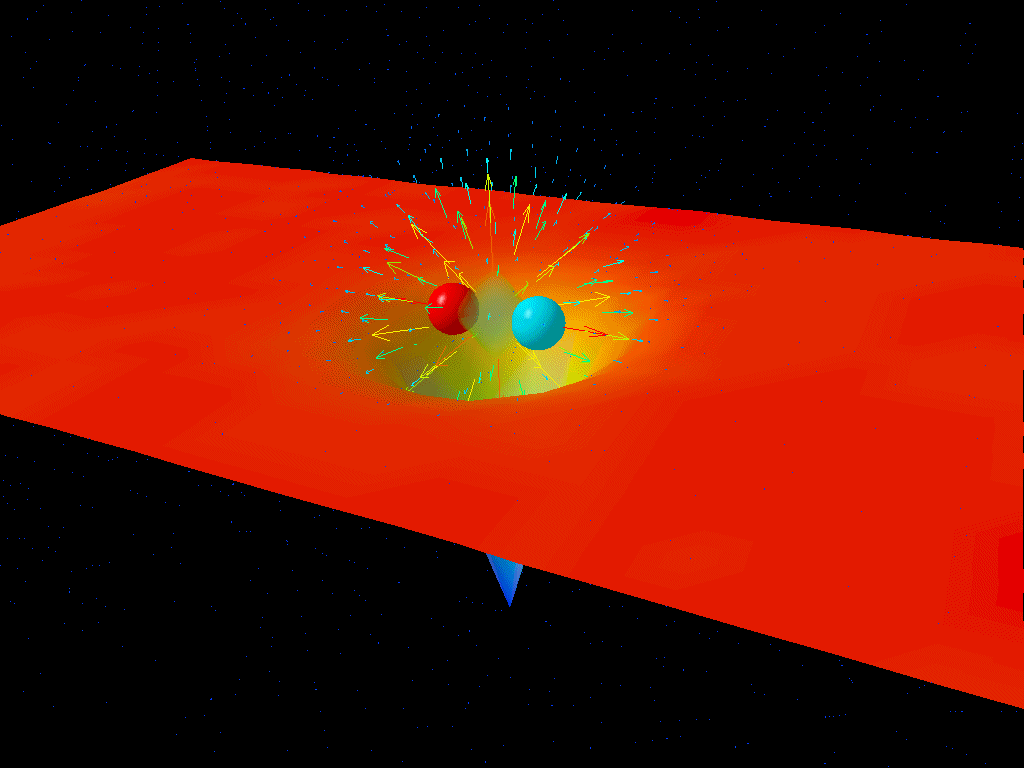
Want to know how two electrically charged particles interact, or how photons interact? That’s governed by quantum electrodynamics, or the quantum theory of the electromagnetic interactions. How about the particles that are responsible for the strong nuclear force: the force that binds protons or other atomic nuclei together? That’s quantum chromodynamics, or the quantum theory of the strong interactions. And what of radioactive decays? That’s the quantum theory of the weak nuclear interactions.

But there are two ingredients missing from this. One’s easy to see: there’s no gravitational interaction listed in the quantum world, because we don’t have a quantum theory of gravity. But another is tougher to see: the three quantum theories we mentioned are normally performed in flat space, or where the gravitational interactions are negligible. (The spacetime that corresponds to this in General Relativity is known as Minkowski space.) However, near a black hole, space is curved and is given by Schwarzschild space, not Minkowski space.

So what happens to these quantum fields not in empty, flat space, but in curved space, like around a black hole? That was the problem that Hawking tackled in 1974, demonstrating that the presence of these quantum fields in the curved space around a black hole causes the emission of thermal, blackbody radiation at a particular temperature. This temperature (and the flux) is lower the more massive the black hole is, due to the fact that the curvature of space is smaller at the event horizon of larger, more massive black holes.

In his popular science book, A Brief History Of Time (still Amazon’s #1 best seller in cosmology), Stephen Hawking described the vacuum of space as consisting of particle/antiparticle pairs of virtual particles, popping in-and-out of existence. Around a black hole, he explained, sometimes one of the two components of these virtual pairs falls in to the event horizon, while the other remains outside. When this happens, he states, the “out” member of the pair escapes with real, positive energy, meaning the “in” member must fall in with negative energy, subtracting from the mass of the black hole and causing it to slowly decay.

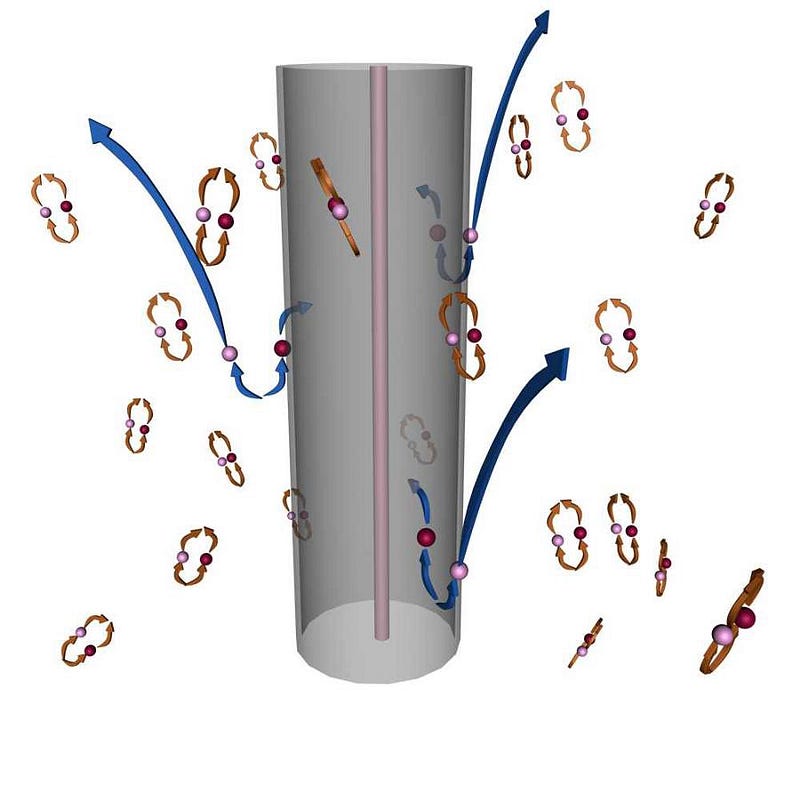
Of course, this picture isn’t right. For starters, the radiation doesn’t come exclusively from the edge of the black hole’s event horizon, but rather throughout the space surrounding it. But the biggest erroneous way of thinking about it like Hawking describes is that the black hole emits photons, not particles and antiparticles, when it comes to this radiation. And in fact, the radiation is of such low energy that it couldn’t produce particle/antiparticle pairs at all.

I, myself, tried to improve on this explanation by emphasizing that these are virtual particles, or a way of visualizing the quantum fields in nature; these are not real particles at all. But these properties of the field can (and do) conspire to produce real radiation.

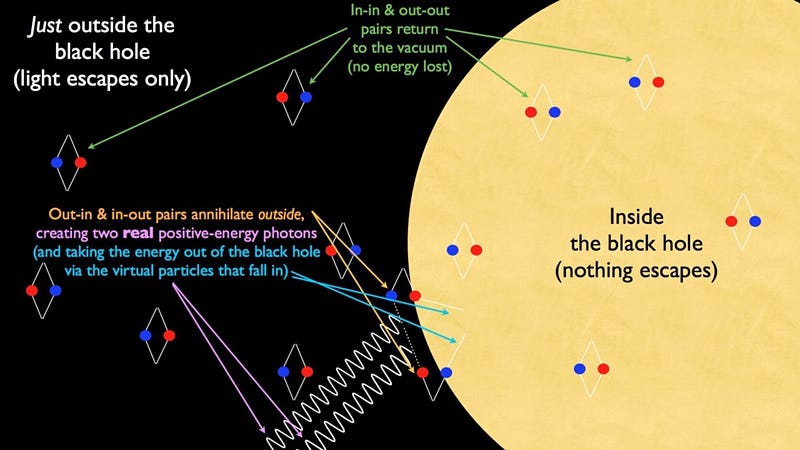
However, this is not quite right, either. It implies that close to the black hole’s event horizon, the radiation is enormous, and only appears small and low in temperature when you’re far away. In reality, the radiation is small at all locations, and only a small percent of the radiation can be traced back to the event horizon at all.

The real explanation is a lot more complex, and shows that this simplistic picture has its limits. The root of the problem is that different observers have different views and perceptions of particles and the vacuum, and this problem is more complicated in curved space than in flat space. Basically, one observer would see empty space, but an accelerated observer would see particles in that space. The origin of Hawking radiation has everything to do with where that observer is, and what they see as accelerated versus what they see as at rest.

When you create a black hole where there was none initially, you are accelerating particles from outside the event horizon to, eventually, inside the event horizon. This process is the origin of that radiation, and Hawking’s calculation showed just how tremendously long the timescale for this emission of evaporative radiation is. For a black hole the mass of the Sun, it will take 10⁶⁷ years to evaporate; for the largest, 10 billion solar mass black holes in the Universe, it will be more like 10¹⁰⁰ years. For comparison, the Universe is only around 10¹⁰ years old today, and the rate of evaporation is so small that it will take around 10²⁰ years before black holes begin evaporating faster than the rate of growth due to the occasional collision with an interstellar proton, neutron or electron.

So the short answer to your question, Spencer, is that Hawking’s picture is totally oversimplified to the point of being wrong. The slightly longer answer is that it’s the infalling of matter itself that causes the radiation, and it’s the extreme curvature of space that causes this radiation to be emitted so slowly, over such long periods of time and over such a large volume of space in the black hole’s vicinity. For even longer, more technical explanations, I recommend (in order of increasing difficulty) Sabine Hossenfelder’s, John Baez’s, and finally Steve Giddings’.

As a fun bonus — and part of our year-end giveaway — Spencer, you need to contact me with your address, because you’ve got a Year In Space 2016 Calendar coming your way! If you want a chance to win, submit your questions and suggestions for the next Ask Ethan here; the selections for the rest of the year will get you a free calendar, too!

Submit your questions and suggestions for the next Ask Ethan here, and if you’re chosen, you’ll win a free Year In Space calendar!

Leave your comments on our forum, support Starts With A Bang here on Patreon, and pre-order our book, Beyond The Galaxy; the 1st chapter is free!