Ask Ethan: How Do Black Holes Actually Evaporate?

Despite what Hawking told you, it really isn’t about particle-antiparticle pairs at all.
Nothing in the Universe lives forever. All the stars that will ever form will someday burn out; distant galaxies and clusters of galaxies get pushed away from one another by dark energy; even the stars within a galaxy, on long enough timescales, will get gravitationally ejected. At the centers of galaxies, though, the largest single objects in the Universe form and grow even today: supermassive black holes. The most massive ones contain tens of billions of solar masses in a singularity surrounded by an event horizon, making them the most massive individual entities we know of. But even they won’t live forever, and Jim Gerofsky wants to know what happens to cause them to die, asking:
[J]ust what is Hawking radiation? The science press articles keep referring to the electron-positron virtual pair production at the event horizon, which makes a lay person think that the Hawking radiation consists of electrons and positrons moving away from the black hole.
As discovered by Stephen Hawking in 1974, black holes eventually evaporate. This is the story of how.

The first thing you have to think about is what empty space truly is. Imagine emptiness as best you can; what would you remove?
You could take all the particles out of it, for starters. Any matter, antimatter, photons, radiation, or anything else you can imagine must all go. You need your space to be devoid of any quanta that could be present, or you won’t be empty.
You’d also have to shield your empty region from the influence of anything outside of it. No electric, magnetic, or nuclear fields (or forces) should be allowed to penetrate it.
Even the gravitational influence of everything else in the Universe would have to be removed. That includes the curvature of space induced by any and all masses and all forms of energy, as well as any gravitational waves — or ripples in spacetime — that could pass through the space you occupy.

In our physical reality, we can’t actually do this, but in theoretical physics, we can imagine it. Imagine a region of space with nothing in it or influencing it at all. The only things you won’t be able to get rid of are spacetime itself, and the laws of physics that govern the Universe.
Yet even if we restrict ourselves to this type of emptiness, when we calculate what’s going on in empty space itself, we find that it’s not so empty. Instead, there’s going to be a certain amount of energy inherent to the fabric of space, owing to the fact that quantum physics is still real. Everything in the Universe has an inherent uncertainty in it: uncertain positions, uncertain momenta, and even and inherently uncertain amounts of energy to it.
Only by averaging everything out, over both time and space, can we obtain any meaningful information at all about what empty space is like.

The energy of empty space itself isn’t something we can theoretically determine in an absolute sense; our calculational toolkit isn’t powerful enough to do it. We can measure the energy inherent to empty space by mapping out the expansion of the Universe, though. The better we measure how the Universe is expanding, the better we constrain the properties of dark energy, which appears to equate to the energy of empty space. It’s the best absolute measurement of the energy density of empty space we have.
And, quite stunningly, that energy density, as much as we might recoil from the conclusion, isn’t zero. The Universe’s expansion is accelerating, and that implies that empty space itself has a positive, non-zero energy density.

So now, replace your empty spacetime with equally empty spacetime, with one exception: you plop down a single, point mass at a location of your choosing.
In technical terms, you’re changing from Minkowski space to Schwarzschild space; in non-technical terms, you’re adding a variable amount of spatial curvature to every location in your Universe. The closer you are to the mass, the more severely spacetime is curved, and there will even be a location where, no matter what type of particle you are or how fast you move or how much you accelerate, escape from within that region is impossible.
The border between being able to escape and not being able to is known as the event horizon, and ought to be a property of all black holes that exist in our Universe.
With all of this in mind, you might start to put some puzzle pieces together, just as Hawking did. Perhaps you’re thinking, “okay, there are all sorts of particles and antiparticles that pop in-and-out of existence, filling empty space. And we now have an event horizon: a region from within which nothing can escape. So occasionally, perhaps, one of the particle pairs that pops into existence outside the event horizon crosses over to be inside the event horizon, before it can annihilate away. The other particle, therefore, can escape, and carry energy away from the black hole as it does.”
Since energy has to be conserved, you might then put together one more puzzle piece, and claim that the energy must come from the mass of the black hole itself. This is very similar to the popular explanation Hawking put forth in explaining Hawking radiation, which details how black holes evaporate.
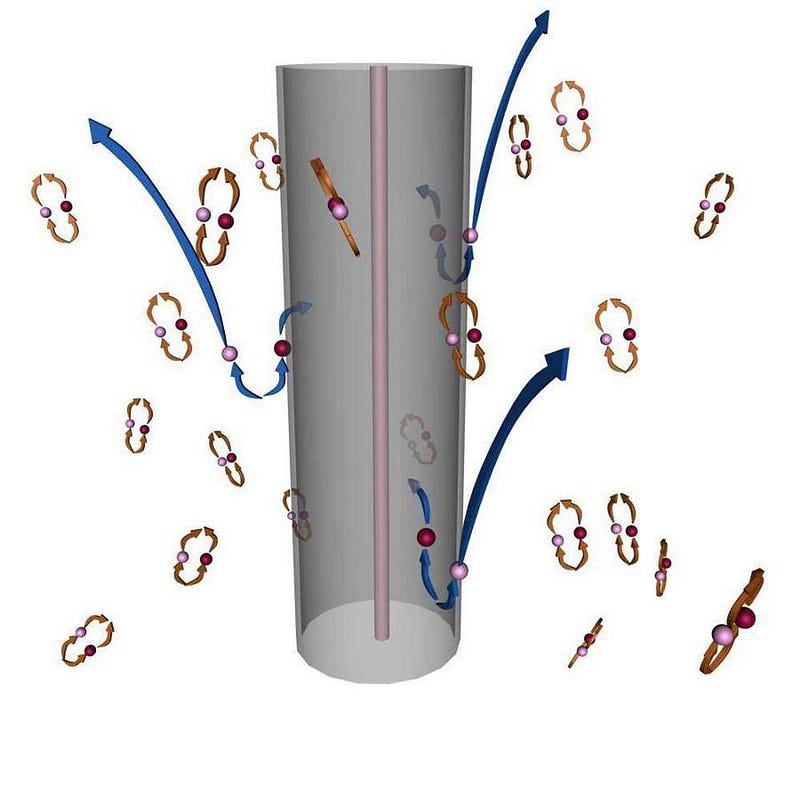
It’s not right, though, in a number of ways. First off, this visualization is not for real particles, but virtual ones. We are trying to describe the quantum vacuum, but these are not actual particles that you can scoop up or collide with. The particle-antiparticle pairs from quantum field theory are calculational tools only, not physically observable entities. Second, the Hawking radiation that leaves a black hole is almost exclusively photons, not matter or antimatter particles. And third, most of the Hawking radiation doesn’t come from the edge of the event horizon, but from a very large region surrounding the black hole.
If you must adhere to the particle-antiparticle pairs explanation, it’s better to try and view it as a series of four types of pairs:
- out-out,
- out-in,
- in-out, and
- in-in,
where it’s the out-in and in-out pairs that virtually interact, producing photons that carry energy away, where the missing energy comes from the curvature of space, and that in turn decreases the mass of the central black hole.
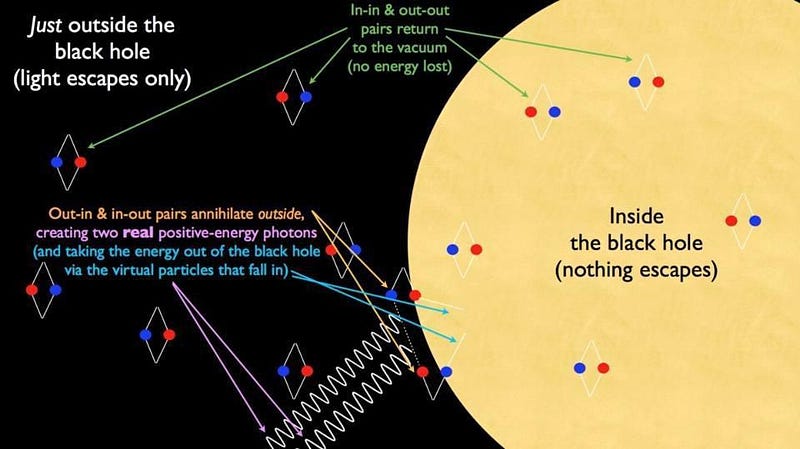
But the true explanation doesn’t lend itself very well to a visualization, and that troubles a lot of people. What you must calculate is how the quantum field theory of empty space behaves in the highly-curved region around a black hole. Not necessarily right by the event horizon, but over a large, spherical region outside of it.
We cannot calculate the absolute energy of empty space, whether it’s curved or uncurved, but what we can do is calculate the difference in the energy and properties of the quantum vacuum between empty and non-empty space.
When you perform the quantum field theory calculation in curved space, you arrive at a surprising solution: that thermal, blackbody radiation is emitted in the space surrounding a black hole’s event horizon. And the smaller the event horizon is, the greater the curvature of space near the event horizon is, and thus the greater the rate of Hawking radiation.

The real explanation is a lot more complex, and shows that the simplistic picture of Hawking has its limits. The root of the problem isn’t that particle-antiparticle pairs are popping in and out of existence, but that different observers have different views and perceptions of particles, and this problem is more complicated in curved space than in flat space.
Basically, one observer would see empty space, but an accelerated observer would see particles in that space. The origin of Hawking radiation has everything to do with where that observer is, and what they see as accelerated versus what they see as at rest.
The result is that black holes wind up emitting thermal, blackbody radiation (mostly in the form of photons) in all directions around it, over a volume of space that mostly encapsulates approximately ten Schwarzschild radii of the location of the black hole.

The big part of Hawking’s explanation that’s correct is that it does imply, given enough time, that black holes will not remain forever, but will decay away.
The loss of energy lowers the mass of the central black hole, eventually leading to total evaporation. Hawking radiation is an incredibly slow process, where a black hole the mass of our Sun would take 10⁶⁷ years to evaporate; the one at the Milky Way’s center would require 10⁸⁷ years, and the most massive ones in the Universe could take up to 10¹⁰⁰ years! And whenever a black hole decays, the last thing you see is a brilliant, energetic flash of radiation and high-energy particles.

Yes, it’s true that Hawking’s original picture of particle-antiparticle pairs produced outside of the event horizon, with one escaping and carrying energy away while the other falls in and causes the black hole to lose mass, is oversimplified to the point of being totally wrong. Instead, radiation is formed outside the black hole owing to the fact that different observers cannot agree on what is happening in the strongly-curved space outside a black hole, and that someone who’s stationary a far distance away will see a steady stream of thermal, blackbody, low-energy radiation emanating from it. The extreme curvature of space is the ultimate cause of this, and results in black holes, very slowly, evaporating away.
Those final decay steps, which won’t occur until long after the final star has burned out, are fated to be the last gasps of energy the Universe has to give off. When the most massive black hole ever to exist finally decays away, it will be the last gasp for new quanta of energy that our Universe, as we know it, will ever create.
Send in your Ask Ethan questions to startswithabang at gmail dot com!
Ethan Siegel is the author of Beyond the Galaxy and Treknology. You can pre-order his third book, currently in development: the Encyclopaedia Cosmologica.