Ask Ethan: Could Octonions Unlock How Reality Really Works?

A fascinating mathematical structure exists that goes well beyond our common experience. Could it revolutionize physics?
Perhaps the most remarkable fact about the Universe is that every particle within it — at all times, locations, and under all conditions — obeys the exact same laws of physics. The rules that nature plays by are the same for everyone, and by finding the mathematical structure that describes those rules, we can describe nature as well. Oftentimes, discovering a new mathematical structure leads to the development of a new physical framework, and where that framework accurately describes the Universe, new physics can be deduced. One of the most fascinating mathematical possibilities for our Universe involves something known as octonions, and that brings us to Patreon supporter Pedro Teixeira’s question, which is:
Octonions, do they stand a chance of being the answer to how our reality works, or just hype?
Let’s start at the beginning: with the mathematics that underlies physics.
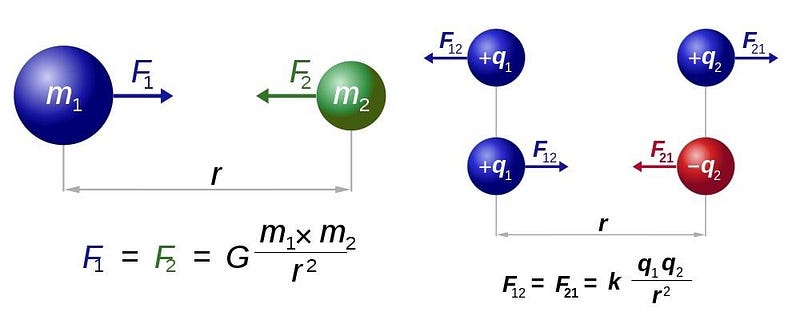
If all you had at your mathematical disposal was the idea of real numbers, you could still get very far. From Galileo to Newton to Coulomb to Maxwell, the entirety of classical physics is built on the basis of real numbers. Force laws, equations of motion, and much more can be derived without resorting to mathematics any more advanced than the set of real numbers, including variables, constants, and dependent functions.
But this already requires a mathematical leap that took millennia to develop: the leap to include negative numbers. When you throw a ball in the air and ask when it will hit the ground, you get two answers for time: one positive and one negative. Sometimes, either answer can be correct, but mathematics alone won’t tell you which situation applies. For that, you need the physical conditions of the problem, and that’s how you decide which answer is the relevant one.
However, real numbers — even when you include both positive and negative numbers — have a limit to the complexity of their mathematical structure. For example, any real number, when you square it, always gives you a positive number, regardless of whether the real number you started with was positive or negative. If you attempt to take a square root of a real number, however, only the positive numbers will give you a real result. The square root of a negative number is not well-defined, not if we restrict ourselves to the set of real numbers, at any rate.
But there’s a new mathematical structure we can add into the fold that gives us the power to not only define the square root of a negative number, but to perform new mathematical operations that are impossible with real numbers alone. This advance required the introduction of a new set of numbers altogether: the imaginary and complex numbers, where the imaginary number i is defined as √(-1).
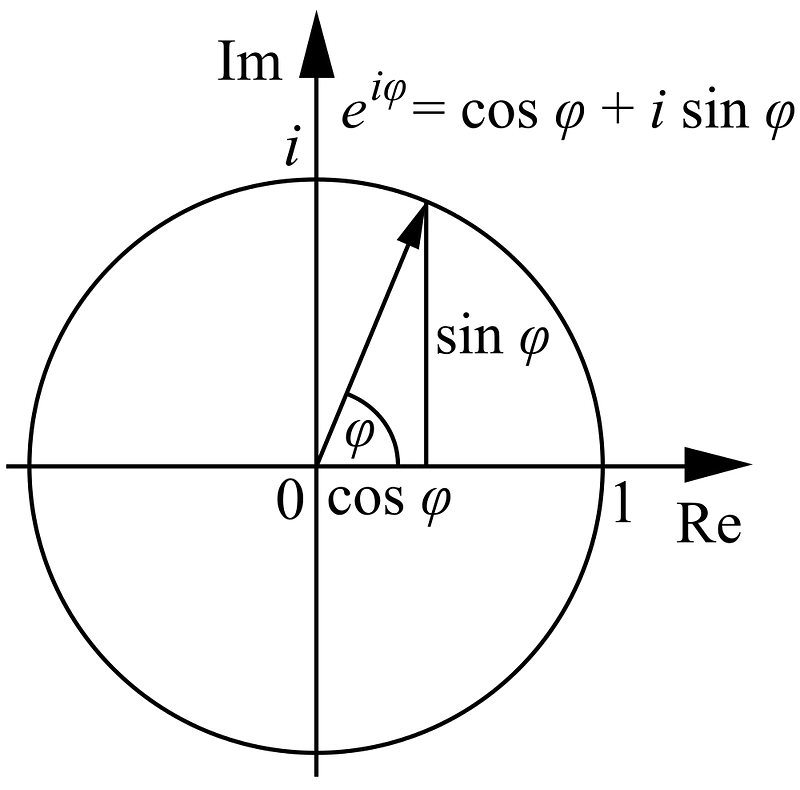
A real number only has a real part, defined by a real number: a. But complex numbers have both a real and imaginary part, a + bi, where a is the real part and bi is the imaginary part. (b is also a real number.) By going from real to complex mathematics (including the mathematics of complex group theory), an entirely new set of physical phenomena could emerge.
Quantum physics took extraordinary advantage of this, noting that the order in which quantum operations were performed made an enormous difference. For real numbers, it doesn’t matter whether you multiply 2 * 3 or 3 *2; you’ll get the same answer. Similarly, for complex numbers, (2 + 5i) * (3–4i) is the same as (3–4i) * (2 + 5i).
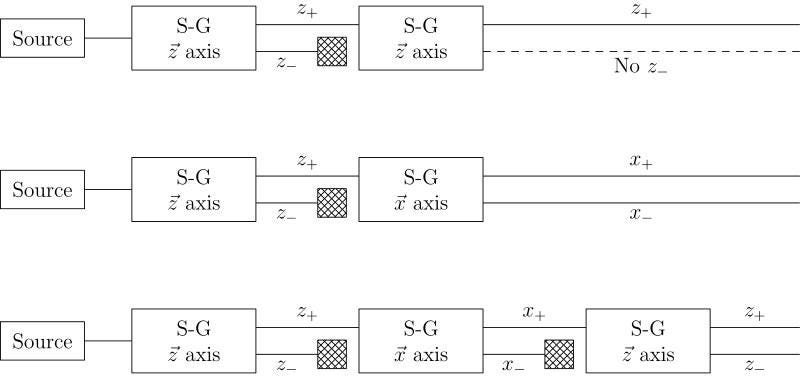
But for quantum operators, order can matter tremendously. If you measure a quantum particle’s spin in the x-direction and then in the y-direction, the particle will have fundamentally different properties than if you measure it in the opposite order. This property — known as non-commutivity — requires complex, rather than real, mathematics (in particular, complex vector spaces) in order to explain it.
The fact that a complex number squared can give you a negative result led to a revolutionary mathematical solution to the Dirac equation, predicting the existence of “negative quantum states.” Dirac initially called these states “holes,” but shortly thereafter, physicists realized what was truly going on: this was the first theoretical prediction of antimatter, in the form of the anti-electron, or positron. Its experimental confirmation was one of the most important discoveries in the development of modern quantum physics.
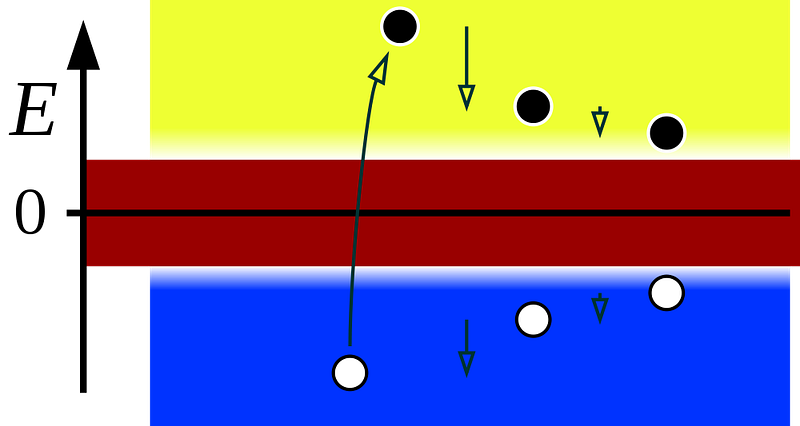
You might think, intuitively, that if you could find a more complicated, more general mathematical structure that extended the complex numbers — the way the complex numbers extended the real ones — you could find a new physical application. If you try to take the square root of a complex number, regardless of whether its real and imaginary parts are either positive or negative, you’ll always still get a complex number. This route won’t lead you to a richer mathematical structure.
But there’s an inherently non-commutative extension you could apply to the complex numbers: instead of letting i² = -1, you can define three independent entities, i, j, and k, where i² = j² = k² = -1, but where the combination i * j * k = -1 also. This fourfold set of factors, where instead of a real number (a) or a complex number (a + bi), you get what’s known as a quaternion: a + bi + cj + dk.
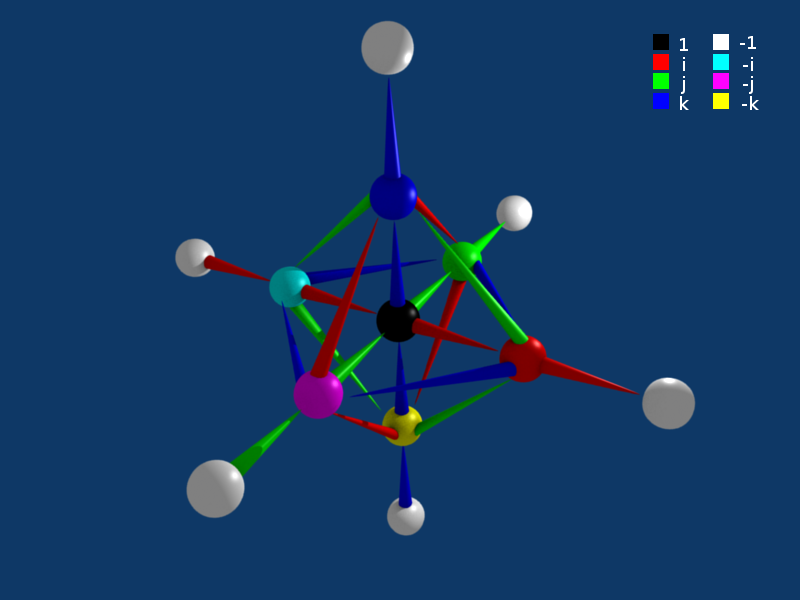
Quaternions are enormously useful in mathematics, but they are also relate to a large number of physical applications. Whereas a complex number represents points in a two-dimensional plane (with a real axis and an imaginary axis), a quaternion has enough dimensions and degrees-of-freedom in it to describe points in three-dimensional space.
The Lorentz transformations, which describe how lengths contract and time dilates as you move close to the speed of light, uses the quaternion group. The General Theory of Relativity can be related to the quaternions in modern algebra. The weak interactions involve quaternions, as do three-dimensional spatial rotations. Certain quantum phenomena are reversed if you rotate your system by 360 degrees, but come back to normal if you do it again and go 720 degrees.
Quaternions are fundamentally non-commutative, and explain why rotating a three-dimensional object about one axis and then another gives you a different final state than rotating that same object about the same two axes, but in the opposite order.

So, you might wonder, can you extend the quaternions even farther? Is there some other way to leverage mathematics where there’s another option available to open up an even richer structure?
The answer is yes, but it comes with a cost. The next step to a more complex mathematical structure is to go from the quaternions to the octonions, which have eight elements apiece, but it comes with a price. For quaternions, multiplication order matters, as Q1 * Q2 is not the same as Q2 * Q1, but the quaternions are still associative. If you have three quaternions (Q1, Q2, and Q3), then (Q1 * Q2) * Q3 = Q1 * (Q2 * Q3). But if you have three octonions, they’re both non-commutative and non-associative; multiplication order not only matters, but it matters in this fundamentally new way.
Whereas the mathematics of quaternions are related to a number of known physical theories, the mathematics of octonions is descriptive of operations that go beyond known physics, describing phenomena that appear in extensions such as Grand Unified Theories (GUTs) and string theory.
Although applications of the octonions to physics are conjectural, there are many good reasons to be interested in these ideas. The octonions teach us, theoretically, how many spacetime dimensions you need to construct a supersymmetric quantum field theory. They are tied to the exceptional Lie groups which are used to construct GUTs and which play a role, through the E(8) group, in superstring theories.
The four classes of numbers we’ve just discussed — the real numbers, the complex numbers, the quaternions, and the octonions — are special in the mathematical field of abstract algebra. These four classes are the only algebras where you can always divide one number by any number other than zero and not get an undefined quantity, making them the only normed division algebras that exist.
If you try to extend the octonions to form a a 16-element algebra, you arrive at the sedenions, which obey their own non-commutative, non-associative multiplication rules, but fail if you try to incorporate division.
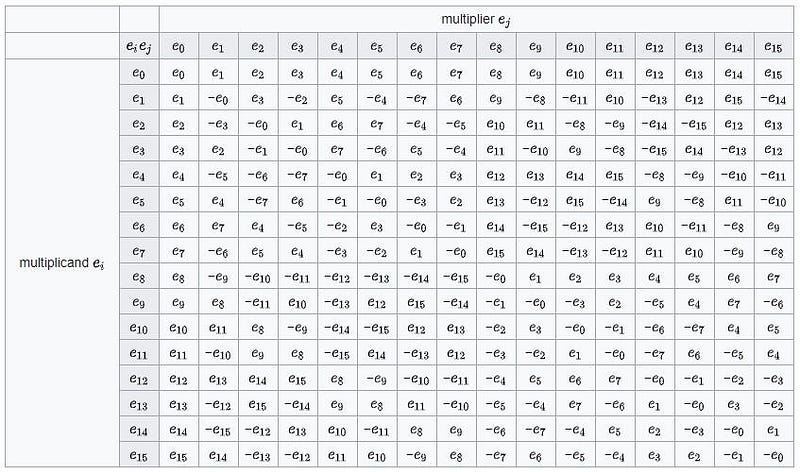
The octonions themselves will never be “the answer” to how reality works, but they do provide a powerful, generalized mathematical structure that has its own unique properties. It includes real, complex, and quaternion mathematics, but also introduces fundamentally unique mathematical properties that can be applied to physics to make novel — but speculative and hitherto unsupported — predictions.
Octonions can give us an idea of which possibilities might be compelling to look at in terms of extensions to known physics and which ones might be less interesting, but there are no concrete observables predicted by the octonions themselves. Pierre Ramond, my former professor who taught me about octonions and Lie groups in physics, was fond of saying, “octonions are to physics what the Sirens were to Ulysses.” They definitely have an allure, but if you dive in, they may drag you to a hypnotic, inescapable doom.
Their mathematical structure holds an incredible richness, but nobody knows whether that richness means anything for our Universe or not.
Send in your Ask Ethan questions to startswithabang at gmail dot com!
Ethan Siegel is the author of Beyond the Galaxy and Treknology. You can pre-order his third book, currently in development: the Encyclopaedia Cosmologica.




