Gaps in the Grammar of the Universe?

Does our grasp of the grammar of the universe have gaps? Is our chosen language in tune with key patterns?
1. The book of the universe is “written in the language of mathematics,” Galileo Galilei declared — God had written two books the Bible and the, “geometrical,” Book of Nature.
2. The Bible’s “in the beginning was the Word,” translates the Greek “logos,” = word, speech/language, reason/logic;logos birthed the organizing binary — cosmos vs. chaos: Language-like rules distinguish order from disorder.
3. For Pythagoreans the cosmos (+ order itself) was “made of numbers.” Critical string-length ratios create harmony (original string theory!), likewise the “music of the spheres” — a heavenly harmony still instrumental for Johannes Kepler and Galileo.
4. Isaac Newton’s Principia Mathematica became the Book of Nature’s rules — enthroning a new mathematical language — natural laws written as algebraic equations. (“Algebra” … Arabic … “reunion of broken parts.”)
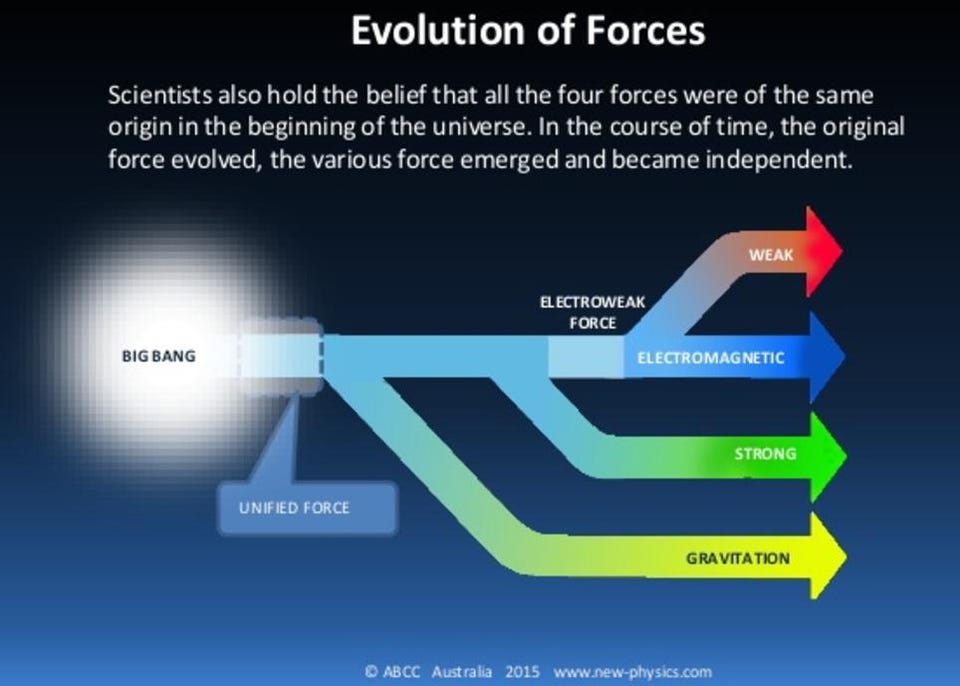
5. Languages develop to fit the domains they describe. The nouns needed in physics have natural sameness — all neutrons are alike. Its verbs enact four forces, in a realm ruled by equal and opposite reactions (third law). Algebra’s symbols and equations perfectly suit such sameness and unchanging interactions.
6. But do Newton’s equal-and-opposite-reaction patterns cover everything under the sun? Is it all translatable into algebra?
7. Nothing in physics chooses. Or varies its reactions. Life chooses (seemingly, even bacteria). Can life’s not-so-mechanical responses be captured by a language fit for physics? Its flux and fuzziness squeezed into patterns lurking “within equations”)?
8. Perhaps different domains have different “freedom quotients” (FQ) … physics’ FQ = 0 … life’s FQ > 0 (begetting contingency patterns).
9. As algebra is to physics, algorithms are to life— recipes for richer response rules, an open generative language of if-then-else step-by-step logic for choosing.
10. Science presumes intelligible patterns. But its default algebraic language can privilege physics-like pattern types. Game theory (= choosology) paints reliable patterns that can’t be solved for algebraically — they must be played out, algorithmically. Simple, fixed choosing rules can generate un-physics-like seemingly chaotic patterns.
11. In Mathematics Without Apologies, Michael Harris depicts working mathematicians chasing timeless universal “Truths” (≠ just “logic in disguise”).
12. Mathematicians (and physicists) fear paradoxes and contradictions, supposedly unsettling “any rational mind.” Less lofty minds routinely handle life’s teeming un-universal, particular, time-bound, partial truths (using algorithm-like scripts).
13. Harris decries seeking an equation for love, his love of mathematics = “ambiguous and resistant to logical formalization” (likewise happiness + much else human).
14. Some believe reality IS mathematics, but mathematics itself isn’t constrained by reality. While physicists imagine a final unifying theory, mathematicians see an endless ladder of abstraction (layers of “avatars” of higher entities).
The issue isn’t the math. It’s presuming that physics-like math is the one true way (the only properly precise language). Mathematics itself needs different languages in its different domains.
“The fault … is not in our stars, but in ourselves” to think their syntax binds us.
May more life-like language (patterns) keep us from “Single vision & Newton’s sleep.”
Illustration by Julia Suits, The New Yorker cartoonist & author of The Extraordinary Catalog of Peculiar Inventions